Nachdem wir letzte Woche das Mandelbrot und Julia-Mengen gemalt haben, wollen wir heute weitere Fraktale produzieren.

Das Ziel

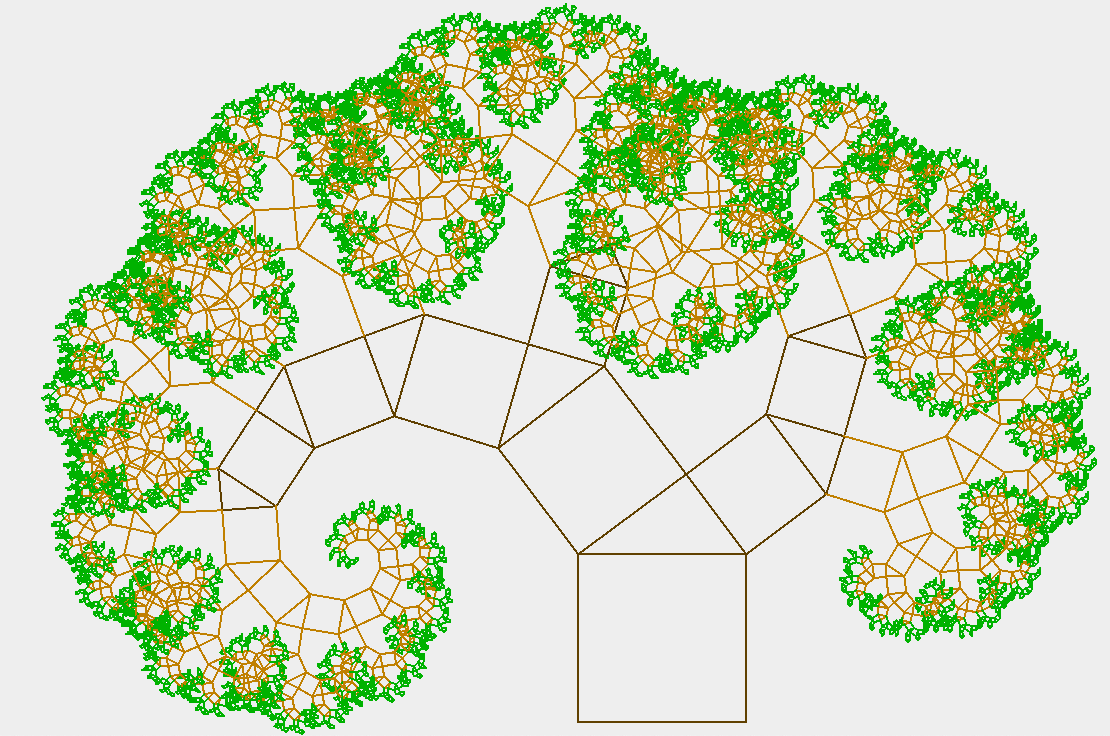
0. Programm aufsetzen

Das kennst du schon: Ein neues Kotlin-Projekt anlegen und das Hauptprogramm ausfüllen, etwa so:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

  class MyWindow(content :JComponent) :JFrame("Baum des Pythagoras") {
    init {
       layout = BorderLayout()
       contentPane = content
       defaultCloseOperation = EXIT_ON_CLOSE
       setSize(800, 600)
    }
  }

  fun main() {
     val window = MyWindow(TreeOfPythagoras())
     window.isVisible = true
  }

1. Komponente zum Malen

Auch diesen Teil solltest du schon einmal gesehen haben. Wir fangen etwa so an:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

  class TreeOfPythagoras() :JComponent {
    companion object {
      val base = Square(0.525, 0.01, 0.125, 0.0)
      val twigSize2 = 0.01
      val leafSize2 = 0.0025
      val cutoffSize2 = 1e-6

      val DARK_BROWN = Color(96, 64, 0)
      val LIGHT_BROWN = Color(192, 128, 0)
      val DARK_GREEN = Color.GREEN.darker()
    }

    private lateinit var scale :Scale

    override fun paint(g :Graphics?) {
      g ?: return
      scale = Scale.of(width.toDouble(), height.toDouble())
      g.color = DARK_BROWN
      drawline(g, base.p0, base.p1)
      branch(base, g)
    }

    fun branch(base :Square, g :Graphics) {
      ...
    }

    fun drawLine(g :Graphics, p0 :Point2D, p1 :Point2D) {
      g.drawLine(scale.px(p0), scale.py(p0), scale.px(p1), scale.py(p1))
    }

    data class Scale(val x0 :Double, val y0 :Double, val dx :Double, val dy :Double) {
      companion object {
        fun of(width :Double, height :Double) :Scale {
          val dx = min(width, height)
          return Scale((width-dx)/2, height -(height-dy)/2, dx, -dx)
        }
      }
    }

    data class Square(val x0 :Double, val y0 :Double, dx :Double, dy :Double) {
      companion Object {
        fun of(x0 :Double, y0 :Double, x1 :Double, y1 :Double)
      }

      val p0 = Point2D(x0, y0)
      val p1 = Point2D(x0+dx, y0+dy)
    }

    data class Point2D(x :Double, y :Double) {}
  }

Die Verwendung von scale sollte dir bekannt vorkommen: Zum Malen müssen wir stets die vituellen Koordinaten in Bildschirm-Koordinaten umrechnen. Dazu legen wir einen gemeinsamen Skalierungsfaktor in $x$- und in $y$-Richtung fest und zentrieren die Ausgabe. Um 2 virtuelle Punkte zu einer Linie auf dem Bildschirm zu verbinden, gibt es die Methode drawLine.

Die Klasse Square beschreibt die Größe des Basiselementes. Dieses besteht aus einem Quadrat (engl. square). Das wiederum besteht aus dem linken unteren Punkt sowie der Richtung der ersten Seite (dx Schritte nach rechts und dy Schritte nach oben). Wir fangen mit einer Standardgröße an, die nur 12.5% des Bildschirms (in jeder Richtung) füllt.

2. Das Basiselement

Wenn wir uns das Zielbild anschauen, erkennen wir, dass der Baum aus einer wiederholten Konstruktion des folgenden Elements besteht:

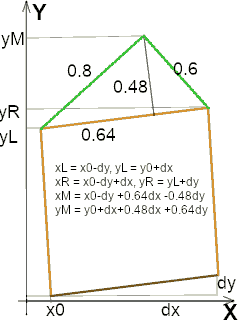
Genau damit fangen wir in der Methode branch (engl. für Zweig/verzweigen) an. Das Stück Stamm ist ein Quadrat, d.h. alle 4 Seitenlängen sind gleichgroß und wir müssen über der gegebenen unteren Seite eine linke, eine obere und eine rechte Seite malen (braune Linien). Dazu ergänzen wir 2 weitere Punkte p2 und p3 in der Definition von Square.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

  class TreeOfPythagoras :JComponent {
    ...

    fun branch(base :Square, g :Graphics) {
      val p2 = base.p2
      drawLine(g, base.p1, p2)
      val p3 = base.p3
      drawLine(g, p2, p3)
      drawLine(g, p3, base.p0)
      ...
    }

    data class Square(...) {
      ...
      val p2 = Point2D(x0+dx-dy, y0+dy+dx)
      val p3 = Point2D(x0-dy, y0+dx)
    }
  }

Dann setzt ein Verzweigungselement auf dem Stück Stamm auf. Das besteht aus einem rechtwinkligen Dreieck. Das einfachste rechtwinklige Dreieck, welches mir einfällt, hat Seitenlängen 3, 4 und 5. D.h. die längste Seite (Hypothenuse) hat Länge 5 und die beiden anderen Seiten Längen 3 und 4, entsprechend. Damit ist tatsächlich $3^2+4^2=9+16=25=5^2$, also ist es ein rechtwinkliges Dreieck.

Wo liegt nun die Spitze?

Die Seite vom linken-oberen Punkt des Quadrates zur Spitze hat die Länge $0.8l$, wobei $l$ die Länge der Seite des Quadrates ist. Wenn das Quadrat $\Delta x$ breit ist, müssen wir $x_0$ um $0.8\cdot0.8\Delta x$ verschieben. Wenn die Grundseite noch um $\Delta y$ rechts angehoben ist, dann muss man die $x$-Koordinate noch um $-0.8\cdot0.6\Delta y$ korrigieren.

Die $y$-Koordinate ist $0.6$ von der Dreiecksseiten-Länge, also $0.8\cdot0.6\Delta x$, wenn die Seite waagerecht liegt. Wenn die Grundseite noch um $\Delta y$ rechts angehoben ist, dann muss die Spitze um $0.8\cdot0.8\Delta y$ zusätzlich angehoben werden.

Insgesamt zeichnet man das Verzweigungselement mittels

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

  ...
  fun branch(base :Square, g :Graphics) {
    ...
    drawLine(g, p3, p0)
    val pT = base.pT
    drawline(g, p3, pT)
    drawLine(g, pT, p2)
  }

  data class Square(...) {
    companion object {
      fun of(...) :Square {...}

      val c = 4.0/5
      val s = 3.0/5
    }
    ...
    private val xT = x0 +c*(c*dx -s*dy)
    private val yT = y0+dx +c*(s*dx+c*dy)

    ...
    val pT = Point2D(xT, yT)
  }

3. Iterum, Iterumque (Wieder und wieder)

Wie kommt man jetzt zu dem gesamten Baum? Dazu muss man auf dem Zweig 2 Zweigelemente aufsetzen. Das kann man wie folgt erreichen:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

  ...
  fun branch(base :Square, g :Graphics) {
    if (base.size2<cutoffSize2)  return
    ...
    branch(Square.of(p3.x,p3.y, pT.x,pT.y))
    branch(Square.of(pT.x,pT.y, p2.x,p2.y))
  }
  ...
  data class Square(...) {
    val size2 = dx*dx +dy*dy
    ...
  }

Die unteren 2 Zeilen malen je Element 2 Kind-Elemente, eines nach links und eines nach rechts. Die obere Zeile braucht man, da sonst das Malen nie fertig wird (unendliche Rekursion). Die Abbruchbedingung ist, dass das Element zu klein ist, um es noch zu sehen.

4. Variationen

4.1 hellbraune Zweige und grüne Blätter

Das kann man dadurch erreichen, dass man bei Eintritt in die branch-Methode die Malfarbe entsprechend der aktuellen Größe setzt, also etwa so

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

  ...
  fun branch(base :Square, g :Graphics) {
    if (base.size2<cutoffSize2)  return
    g.color = when {
      base.size2<leafSize2 -> DARK_GREEN
      base.size2<twigSize2 -> LIGHT_BROWN
      else -> DARK_BROWN
    }
    ...
  }

4.2 Zufällige Drehung

Diese kann man erreichen, indem man den Dreieckspunkt wahlweise nach links oder nach rechts verschiebt. Die Koordinaten zur Verschiebung nach links lauten: $0.6(0.6\Delta x-0.8\Delta y)$, $0.6(0.8\Delta x+0.6\Delta y)$.

Die zufällige Flunktuation kann man erreichen, indem man

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

  val random = random()

  class TreeOfPythagoras() :JComponent {
    ...
    data class Square(val x0 ... :Double, val moveRight :Boolean = random.nextBoolean()) {
      ...
      val xT = if (moveRight) c*(c*dx -s*dy)  else s*(s*dx -c*dy)
      val yT = if (moveRight) c*(s*dx +c*dy)  else s*(c*dx +s*dy)
      ...
    }
    ...
  }

4.3 Weniger Zweige

Das kann man erreichen, indem man den 2. (kleineren) Zweig nur manchmal einfügt, z.B. so

1
2
3
4
5
6
7

  fun branch(base :Square, g :Graphics) {
    ...
    if (rect.moveRight||random.flipCoin(0.8))
        branch(Rect.of(p3.x,p3.y, pt.x,pt.y), g)
    if (!rect.moveRight||random.flipCoin(0.8))
        branch(Rect.of(pt.x,pt.y, p2.x,p2.y), g)
  }

9. Selber Probieren

Jetzt bist du dran. Funktioniert das Programm bei dir? Falls nicht, schau doch mal auf die Fehlermeldung, vielleicht bekommst du wenigstens heraus, wo der Fehler ist. Dann musst du die entsprechende Stelle verstehen und korrigieren.

Kannst du den Baum so abändern, dass der Stamm-Bereich (size2>=twigSize2) grau-braun ist?

9.2 Anderes Dreieck

Was passiert, wenn du die Seitenverhältnisse des Dreiecks auf 12.0/13 und 5.0/13 änderst? (Eventuell musst du das Anfansquadrat noch etwas nach rechts verschieben.)

9.3 3 Zweige

Was müsstest du ändern, damit nicht 2 Zweige, sondern 3 Zweige von jedem Stammstück abgehen?

Hinweis: Offenbar muss der rekursive Aufruf am Ende 3-mal kommen. Welchen 2. Stützpunkt kann man wählen?

Viel Spaß beim Probieren.