After we have been drawing moving eyes last time, we want to draw something more interesting.

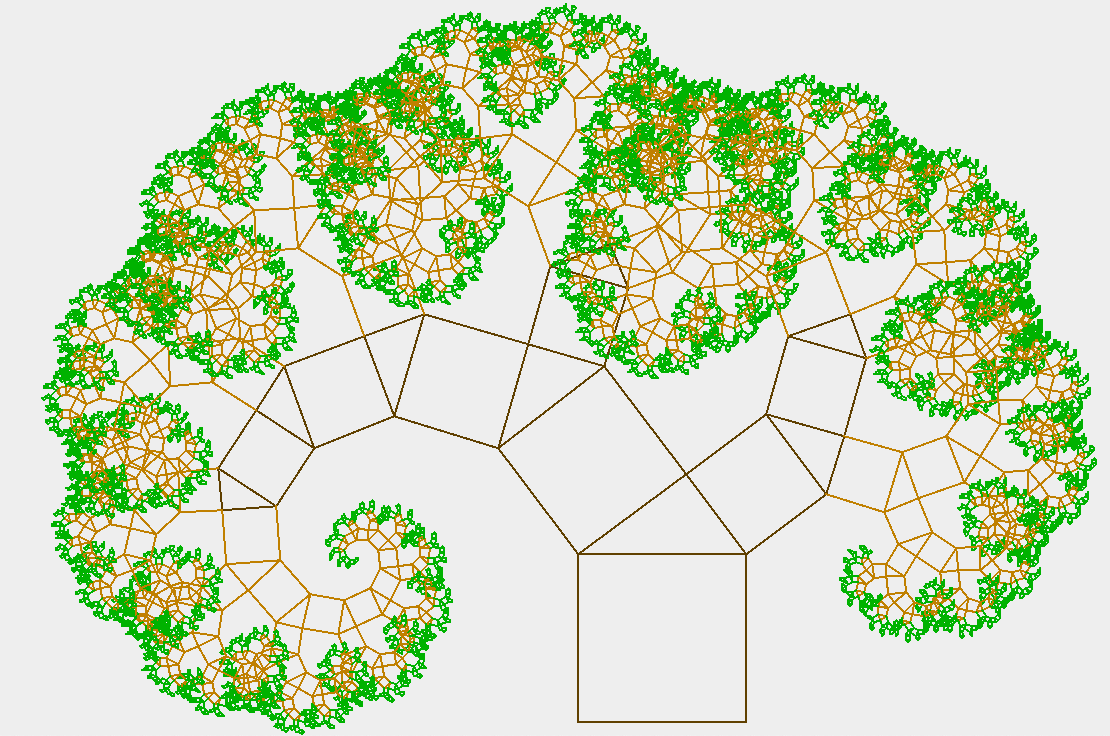
Our Goal

Tree of the Pythagoras

1. Setting up the Project

With the QtCreator, you create a New Project … of type C++ Qt Widget Application. Give a memorizable name to the project, e.g. pythagoreanTree (毕达哥拉斯的树), but make sure the Build-System is cmake/minGW11. Call the main window “PythagorasTreeWidget” and make it derive from QWidget. We don’t need to choose any translation language (as our app will not contain much text).

After a while, the IDE opens the file “main.cpp” with a minimal Qt main program. You can even reduce this as follows:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


#include "eyewidget.h"

#include <QApplication>

int main(int nArgs, char* args[])
{
    QApplication app(nArgs, args);

    EyeWidget w;
    w.show();
    return app.exec();
}

This is all we need here.

Next, we need to make sure, the header file is set up properly. It should look as follows:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


#ifndef PYTHAGORASTREEWIDGET_H
#define PYTHAGORASTREEWIDGET_H

#include <QWidget>

class PythagorasTreeWidget : public QWidget
{
    Q_OBJECT

public:
    explicit PythagorasTreeWidget(QWidget* parent = nullptr);
    ~PythagorasTreeWidget() override;

    void paintEvent(QPaintEvent*) override;
};
#endif // PYTHAGOREANTREEWIDGET_H

1.2 The main Element

Trunk and Fork

The drawing happens in the “pythagorastreewidget.cpp” file. We start as follows:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42



#include "pythagorastreewidget.h"
#include <QtGui>

PythagorasTreeWidget::PythagorasTreeWidget(QWidget* parent)
        : QWidget(parent) {
    setMinimumSize(160, 120);
    setWindowTitle(tr("Tree of Pythagoras"));
    setMouseTracking(true);
}

PythagorasTreeWidget::~PythagorasTreeWidget() = default;

struct Rect {
    double x0, y0, dx, dy;
};

void sprout(QPainter& p, const Rect& base, int depth =10) {
    if (depth<1)
        return;

    p.drawLine(int(base.x0), int(base.y0), int(base.x0+base.dx), int(base.y0+base.dy));

    const double xl = base.x0-base.dy;
    const double yl = base.y0+base.dx;
    p.drawLine(int(base.x0), int(base.y0), int(xl), int(yl));

    const double xr = base.x0 +base.dx -base.dy;
    const double yr = base.y0 +base.dx +base.dy;
    p.drawLine(int(xl), int(yl), int(xr), int(yr));
    p.drawLine(int(xr), int(yr), int(xr+base.dy), int(base.y0+base.dy));

    ...
}

void TreeWidget::paintEvent(QPaintEvent*) {
    auto p = QPainter(this);
    p.setPen(QColor("brown"));
    const Rect base = { 0.65*width(), 0.95*height(), -0.14*width(), 0.0 };
    sprout(p, base);
    p.end();
}

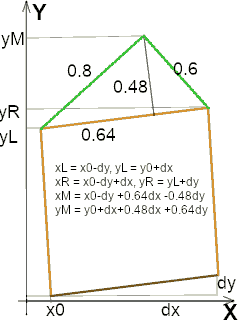
A struct is a tuple of variables that is given a typename. Here we define a Rect (from rectangle) that consists of a left point $(x_0, y_0)$, some width $dx$ and some height $dy$. In the paintEvent(...)-method, we compute some static (rather small) line segment and hand that to the sprout function. Sprout (发芽) is the process when a new twig or leaf grows on a branch (or tree). We will see later, why we need a separate function for that. In addition, we need to pass a QPainter to the function, but we don’t want it to be copied everytime. Therefore we pass it by reference. The same way, we also pass the rectangle via reference (and make it constant, i.e. unchangeable).

You should try that part by starting the program and see whether it really draws a trunk (in black).

2. Iterum, iterumque

OK, we have drawn a trunk, but how do we make it a whole tree with many branches and small leaves?

The answer is that we sprout the same element again and again over the 2 segments on top (the green ones in Picture 1). First, let us compute the left segment and recurse there:

1
2
3
4
5
6



void sprount(QPainter& p, const Rect& base, int depth =10) {
    ...

    Rect left = { xl, yl, 0.36*base.dx-0.48*base.dy, 0.48*base.dx+0.36*base.dy };
    sprout(p, left, depth-1);

If you restart the program, you will see the left lowest branches that extend along the whole tree.

If we want to make the leaves green, we should compute the sprout size and set the color correspondingly.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23



template <typename F>
F sqr(F x) {
    return x*x;
}

const QColor lightGreen = QColor(128, 255, 0);
const QColor lightBrown = QColor(192, 128, 0);
const QColor darkBrown = QColor(96, 48, 0);

void sprout(QPainter& p, const Rect& base, int depth =10) {
    const double size2 = sqr(base.dx)+sqr(base.dy);
    if (size2<4.0||depth<1)
        return;
    if (size2<36.0)
        p.setPen(lightGreen);
    else if (size2<1024.0)
        p.setPen(darkGreen);
    else
        p.setPen(darkBrown);

    ...
}

This is called a recursive function (递归函数), i.e. the function sprout calls itself in order to produce the whole result. For a recursive algorithm two things are important: First, you need to know when to stop the recursion. If you forget the stopping condition (or if it fails), then the algorithm will never terminate. Secondly, you need solve one step of the problem and finally call the function itself again handing over a smaller part of the problem.

If you restart the program, you will see the trunk in dark-brown, the branches to the side in light-brown and the leaves in light-green.

2.2 To the Right

Next, we will extend the branches to the right. But before the program fills the whole screen, we will temporarily disable the left branches. This looks about as follows:

1
2
3
4
5
6


void sprout(QPainter& p, const Rect& base, int depth =10) {
    ...
    // sprout(p, left, depth-1);
    Rect right = { xl+left.dx, yl+left.dy, xr-(left.x0+left.dx), yr-(left.y0+left.dy) };
    sprout(p, right, depth-1);
}

When you start the program again, you will see a long branch to the right that ends in a light-green leaf. Make sure, the branch becomes smaller and smaller.

Once, we have convinced ourselves that both recursions work properly for themselves, we can enable them both at the same time, i.e. comment-in the first sprout() call.

This is now called a double recursive function (双重递归函数), i.e. every (full) iteration of the function calls the function itself twice.

When you now restart the program, you should see the whole tree.

Try to resize the window and find out when the tree fills the whole window. You may also wish to switch the window to full-screen. If you want to save the tree to an image, you just have to press <Win>+<P> (or <cmd>+<shift>+<4> on Mac).

If you get the impression that the leaves are not drawn in maximum zoom, then you can remove the depth condition in the first if-statement:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10



void sprout(QPainter& p, const Rect& base) {
    const double size2 = sqr(base.dx) +sqr(base.dy);
    if (size2<4.0)
        break;
    ...
    sprout(p, left);
    const Rect right = {...};
    sprout(p, right);
}

9. Try for Yourself

The tree is slightly left-leaning, i.e. the left branches are always a bit bigger than the right branches on the same level.

Can you reflect the tree, i.e. exchange the sizes of the left and the right branches?

Hint: You may have to move the middle point $(x_M, y_M)$ more to the right, e.g. with the factors $0.48$ and $0.36$ (you should change 4 numbers). Does it work?

12CE Tree of Pythagoras

Contents