Nachdem wir in den ersten 3 Teilen eine Einführung in Kotlin und Programmieren, sowie Grafikprogrammierung und vertiefende Algorithmen betrachtet haben, wollen uns jetzt mittelgroßen Projekten widmen. Heute fangen wir mit Bézierkurven an.

0. Die Aufgabe

Gegeben ein paar Punkte in der Ebene, wie können wir eine glatte Kurve durch diese Punkte zeichnen?

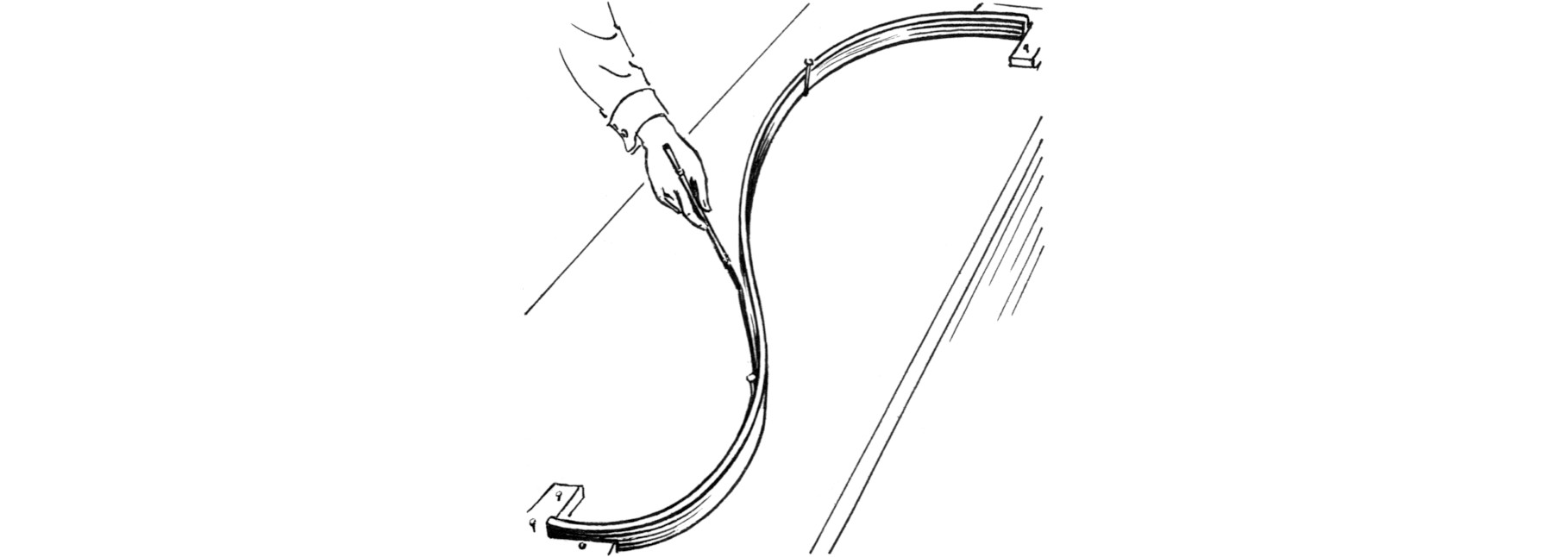Bild 1: Straklatte (engl. spline) durch 4 Punkte. CC SA P.S. Foresman 2007.

Wenn wir das mechanisch tun wollen, dann könnten wir die benachbarten Punkte mit einem Lineal (und Stift) verbinden. Wenn wir aber eine glattere Kurve (ohne Ecken) haben wollen, dann können wir vielleicht eine Straklatte (englisch spline) verwenden. Diese wird an 2 Punkten eingespannt und an 2 weiteren Punkten dazwischen abgestützt. Dann kann man mit einem Stift (oder Cutter) eine Kurve entlang des Bands ziehen. Wenn man das ganze mehrfach ansetzt und dabei die Punkte der Reihe nach durchgeht, dann erhält man eine glatte Kurve durch alle Punkte. Als Ergebnis kann man etwa das Folgende erhalten.

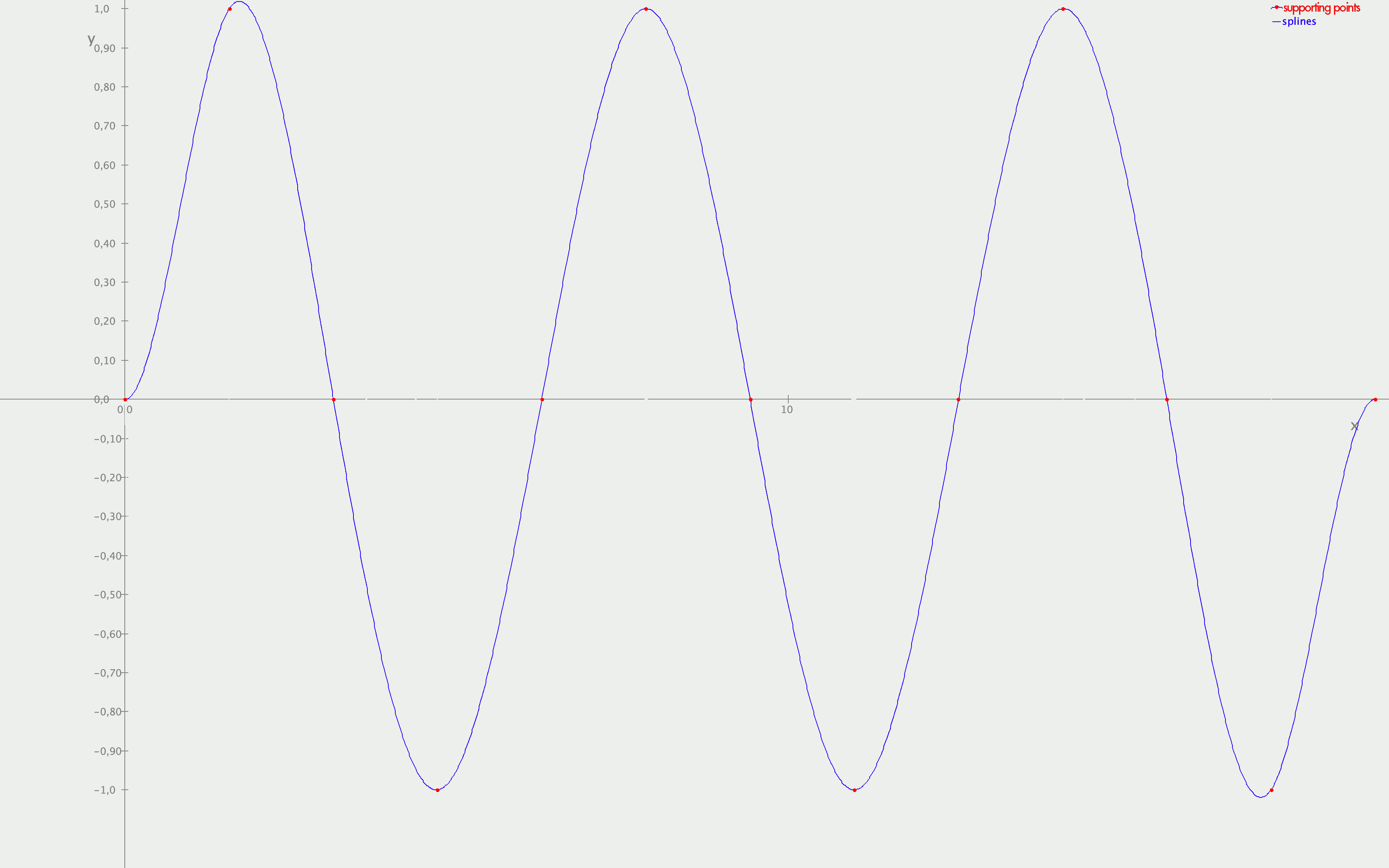
Eine glatte Kurve durch ein paar Punkte. CC Att M. Grützmann 2023.

Bild 2: Eine glatte Kurve durch ein paar Punkte. CC Att M. Grützmann 2023.

Die Frage ist, wie man das im Computer durchführen kann.

Als Literatur kann man [1] oder [2] verwenden. Ich gebe hier eine minimale Zusammenfassung.

[1] wiki: Bézierkurven

[2] L.L. Schumaker: Spline Functions, Basic Theory, 1981.

1. Vollständige Interpolation

Gegeben seien $n+1$ Punkte mit den Koordinaten $(x_0,y_0)$ bis $(x_n, y_n)$. Wir können einfach ein Polynom n-ten Grades durch diese Punkte legen, so wie wir das letztens bei den Fehlerkorrektur-Codes getan haben. Dazu müssen wir das lineare Gleichungssystem $X\mathbf a = \mathbf y$ lösen. Wir hatten festgestellt, dass die Matrix $$ X = \begin{pmatrix} 1 & x_0 & x_0^2 & \dots & x_0^n \\ 1 & x_1 & x_1^2 & \dots & x_1^n \\ \vdots && & & \\ 1 & x_n & x_n^2 & \dots & x_n^n \end{pmatrix} $$ darüber entscheidet, ob das Gleichungssystem eindeutig lösbar ist. Die rechte Seite ist der Vektor $\mathbf y = (y_0, y_1, \dots,y_n)^T$ und die Unbekannten sind die Koeffizienten $\mathbf a = (a_0, a_1,\dots, a_n)^T$.

Solange wird die Stützstellen $x_0, x_1,\dots, x_n$ alle verschieden wählen, ist das Gleichungssystem eindeutig lösbar. (Die Koeffizienten $X$ sind die van der Monde Matrix und deren Determinante ist die van der Monde Determinante.)

Die Frage ist, wie gut das ist. Dazu könnten wir die Größe

$$ \mathrm{RMSE} = \left[\int_a^b \left(f(x)-p(x)\right)^2\,dx\right]^{1/2} $$

ausrechnen. Allerdings müssen wir die Originalfunktion $f\colon[a,b]\to\mathbb R$ an mehr als den $n+1$ Stellen kennen, denn an diesen Stellen ist die Differenz 0 (bis auf Rundungsfehler).

Alternativ können wir das Ergebnis der Orginalfunktion $f$, der Interpolation $p$ und vielleicht des Fehlers error$(x)= p(x)-f(x)$ plotten. Da wir sowieso einige Ergebnisse darstellen wollen, entwerfen wir gleich mal ein Programm, um reelle Funktionen zu plotten.

2. Ein Funktionen-Plotter

Da wir bereits mit Swing umgehen können, schreiben wir ein Programm mit Swing, in dem eine reelle Funktion dargestellt wird. Das kann etwa wie folgt losgehen:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


  class MyWindow(content :JComponent) :JFrame("Function Plotter") {
    init {
      this.layout = BorderLayout()
      this.contentPane = content
      setSize(800, 600)
      defaultCloseOperation = EXIT_ON_CLOSE
    }
  }

  fun main() {
    val n = 5
    val xs = (-n..n).map { i -> (i.toDouble()/n) }.toDoubleArray()
    val domain = DoubleRange(-1.0, 1.0)
    val f = DescribedFunction("1/(1+x^2)") { x -> 1/(1+x*x) }
    val window = MyWindow(Plotter(f, domain))
    window.isVisible = true
  }

Dazu haben wir bereits ein paar Abstraktionen eingeführt:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


  @OptIn(ExperimentalStdlibApi::class)
  data class DoubleRange(override val start :Double, override val endExclusive :Double) :OpenEndRange<Double> {
    val width = endExclusive - start

    init {
      assert(start<endExclusive)
    }

    fun partition(n :UInt) :DoubleArray {
      val dx = width/n.toInt()
      return (0u..n).map { i -> start +dx*i.toInt() }.toDoubleArray()
    }
  }

Ein DoubleRange ist ein Interval, d.h. es hat einen Startpunkt und einen Endpunkt. Englisch exclusive heißt ausgeschlossen, d.h. dass der Endpunkt selbst nicht zum Interval gehört. Eine Partition ist eine Unterteilung des Intervals in $n+1$ Punkte, wobei der 0. Punkt der Startpunkt ist und der $n$-te Punkt der Endpunkt ist. Wir wollen hier äquidistant unterteilen, d.h. alle Zwischenpunkte sind voneinander gleichweit entfernt.

1
2
3


  data class DescribedFunction(val name :String, val f :(Double)->Double) {
    fun f(xs :DoubleArray) = xs.map { x -> f(x) }.toDoubleArray()
  }

D.h. eine beschriebene Funktion besteht aus dem Funktionsnamen und der Vorschrift, wie man aus x den Funktionswert berechnet. Wir implementieren gleich noch eine Methode, die wir auch f nennen, die aus einem Vektor von x-Werten gleich den Vektor der y-Werte berechnet.

Wie sieht nun der Plotter aus?

Ein erster Entwurf könnte wie folgt sein:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82


  class Plotter(val fs :List<DescribedFunction>, val domain :DoubleRange =DoubleRange(0.0, 1.0)) :JComponent() {
    companion object {
      val colors = listOf(Color.BLACK, Color.BLUE, Color.GREEN.darker(), Color.RED, Color.ORANGE.darker(),
        Color.CYAN.darker(), Color.MAGENTA.darker())
    }

    private var n = 1024u
    private lateinit var xs :DoubleArray
    private lateinit var range :DoubleRange
    private val ys = mutableListOf<DoubleArray>()
    private lateinit var scale :Scale

    init {
      assert(fs.isNotEmpty())
      recompute(1024u)
      val ym = ys.minOf { it.min() };  val yM = ys.maxOf { it.max() }
      range = DoubleRange(ym, yM)
    }

    fun recompute(n :UInt) {
      this.n = n
      xs = domain.partitition(n)
      ys.clear()
      fs.forEach { f ->
        ys.add(f.f(xs))
      }
    }

    override fun paint(g :Graphics) {
      scale = computeScale(width, height)
      g.drawAxes()
      g.drawCurves()
      g.drawLabel()
    }

    private fun Graphics.drawCurves() {
      ys.forEachIndexed { k, ys1 ->
        color = colors[k % colors.size]
        var x0 = scale.px(xs[0])
        var y0 = scale.py(ys1[0])
        xs.zip(ys1).forEach { (x, y) ->
          val x1 = scale.px(x)
          val y1 = scale.py(y)
          drawLine(x0,y0, x1,y1)
          x0 = x1;  y0 = y1
        }
      }
    }

    private fun Graphics.drawLabel() {
      val x = width -150
      var y = 16
      fs.forEachIndexed { k, f ->
        color = colors[k % colors.size]
        drawLine(x, y-4, x+10, y-4)
        drawString(f.name, x+12,y)
        y += 16
      }
    }

    private fun Graphics.drawAxes() {
      color = Color.GRAY
      val x0 = scale.px(0.0)
      drawLine(x0,0, x0,height)
      drawString("y", x0-16, 16)

      val y0 scale.py(0.0)
      drawLine(0,y0, width,y0)
      drawString("x", width-50, y0-16)
    }

    fun computeScale(width :Int, height :Int) :Scale {
      val dx = width/domain.width*0.9;  val dy = height/range.width*0.9
      return Scale(domain.start -(width/dx-domain.width)*0.45,
        range.endExclusive +(height/dy-range.height)*0.45, dx, -dy)
    }

    data class Scale(val x0 :Double, y0 :Double, dx :Double, dy :Double) {
      fun px(x :Double) = ((x-x0)*dx).roundToInt()
      fun py(y :Double) = ((y-y0)*dy).roundToInt()
    }
  }

Was macht diese Klasse?

Naja, zur Initialisierung übergibt man eine Liste DescribedFunctions, d.h. Funktionen mit Namen, einen Definitionsbereicht (engl. domain) und dann wird eine Partition des Definitionsbereiches in n=1024 Stellen berechnet und zu diesen $n+1$ Stellen die y-Werte und das für alle übergebenen Funktionen.

Die grafischen Aktionen werden von der paint(...)-Methode ausgeführt und sind zunächst das Neuberechnen der Skala, das Malen der Axen, das Malen der Kurven und dann noch das Malen einer Legende (engl. label).

Dir Kurven werden in der oben definierten Farbskala gemalt, d.h. die erste Kurven in schwarz (engl. BLACK), dann blau (engl. BLUE), dunkelgrün (engl. GREEN und darker() heißt dunkler), rot (engl. RED), orange, türkis (engl. CYAN), violett (engl. MAGENTA). Falls mehr als 7 Kurven angegeben sind, dann wird wieder von vorn begonnen mit der Farbskala.

Die Berechnung der Skalierung sollte dir schon bekannt vorkommen. In diesem Falle skalieren wir die x- und die y-Achse unabhängig, da ja nicht klar ist, dass Definitions- und Wertebereich gleichgroß sind.

Wenn man die x-Achse einzeichnen will, dann muss man zunächst herausfinden, bei welcher y-Koordinate, die eingezeichnet werden muss. Die Antwort ist y0 = scale.py(0.0), d.h. bei $y=0$ aber eben in Bildschirmkoordinaten. Entsprechend muss man die y-Achse bei x0 = scale.px(0.0) einzeichnen.

Schließlich besteht die Legende (engl. label) aus den Namen (f.name) in den Farben der Kurven. Dazu müssen wir einen Text in das Grafikfenster malen, drawText(txt, px,py). Ich habe entschieden, dass die Legende rechts-oben sein soll, also 150 Punkte links vom rechten Rand val x = width -150 und beginnend 16 Punkte vom oberen Rand var y = 16. Beim malen eines Textes muss man die linke untere Ecke von Text angeben, d.h. man kann nicht einfach width, 0 angeben, da sonst der Text außerhalb des Bildschirms liegt.

Kann man das jetzt schon testen? – Probier’s aus!

Leider kompiliert es nicht. Das wichtigste Problem (wenn du alle Teile fehlerfrei abgetippt hast und die entsprechenden Symbole importiert hast) ist, dass zum Erzeugen des Plotters man eine Liste von DescribedFunction übergeben muss, wir aber nur 1 Funktion malen wollen. Was kann man da machen?

Wir könnten den Aufruf anpassen, sodass statt Plotter(f, domain) einfach Plotter(listOf(f), domain) übergeben wird. Andererseits können wir auch Kotlin mitteilen, dass wenn nur eine Funktion übergeben wird, diese automatisch in eine Liste umgewandelt werden soll. Wie kann man das machen?

Dazu ergänzen wir einen 2. Konstruktor in der Klasse Plotter (vor der init-Methode), wie folgt:

1

  constructor(f :DescribedFunction, domain :DoubleRange) :this(listOf(f), domain)

Die Notation :this(...) ist etwas speziell. Sie besagt, dass die Klasse wie üblich initialisiert wird. Dazu müssen wir aber die üblichen Argumente übergeben, also eine Liste von DescribedFunction und den Definitionsbereich, den wir ja erhalten hatten.

Wichtig wäre, dass du die Funktionsweise erst einmal testest, um dich davon zu überzeugen, dass dieser Teil bereits funktioniert.

3. Lösen von linearen Gleichungssystemen

Um jetzt die Interpolation vom Anfang zu malen, muss man das entsprechende lineare Gleichungssystem lösen. Dazu können wir etwa Matrizen (reeller Zahlen) definieren und den Gauß-Algorithmus vom letzten Mal verwenden. Das sieht etwa wie folgt aus:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99


  data class RMatrix(private val cs :DoubleArray, val n :UInt) :Clonable {
    val m = cs.size.toUInt()/n

    init {
      assert(m*n == cs.size.toUInt())
    }

    override fun clone() = RMatrix(cs.clone, n)

    override fun toString() = "(" + (0u until m).map { r ->
        (r *n until (r +1u) *n).map { offset -> cs[offset.toInt()] }.joinToString()
    }.joinToString(")\n(") + ")"

    operator fun get(r :UInt, c :UInt) = cs[(r*n).toInt() +c.toInt()]

    operator fun set(r :UInt, c :UInt, value :Double) {
      cs[(r*n).toInt() +c.toInt()] = value
    }

    fun slice(r :UInt) = cs.slice((r * n).toInt() until ((r + 1u) * n).toInt())

    fun copy(pad :UInt) = RMatrix((0u until m).flatMap { r -> slice(r) +(1u..pad).map { 0.0 } }.toDoubleArray(), n+pad)

    fun paste(r0 :UInt, c0 :UInt, ys :DoubleArray) {
        assert(r0 + ys.size.toUInt() <= m)
        ys.forEachIndexed { k, y -> set(r0 +k.toUInt(), c0, y) }
    }

    fun swap(r :UInt, r0 :UInt) {
        if (r == r0)
            return
        assert(r < m && r0 < m)
        val offset = (r * n).toInt()
        val offset0 = (r0 * n).toInt()
        for (c in 0 until n.toInt()) {
            val tmp = cs[offset + c]
            cs[offset + c] = cs[offset0 + c]
            cs[offset0 + c] = tmp
        }
    }

    fun scale(r :UInt, f :Double) {
        val offset = (r * n).toInt()
        for (c in 0 until n.toInt())
            cs[offset + c] *= f
    }

    fun add(r0 :UInt, r :UInt, f :Double) {
        val offset0 = (r0 * n).toInt()
        val offset = (r * n).toInt()
        for (c in 0 until n.toInt())
            cs[offset +c] += cs[offset0 +c] * f
    }

    operator fun times(f :Double) = RMatrix(cs.map { c -> c * f }.toDoubleArray(), n)

    fun transpose() = RMatrix((0u until n).flatMap { c -> (0u until m).map { r -> get(r, c) } }.toTypedArray(), m)

    operator fun times(f :RMatrix) :RMatrix {
        assert(n == f.m)
        val result = (0u until m).flatMap { r ->
            (0u until f.n).map { c ->
                (0u until n).toList().sumOf { k -> get(r, k) * f[k, c] }
            }
        }
        return RMatrix(result.toTypedArray(), f.m)
    }

    operator fun times(ys :DoubleArray) :DoubleArray {
        assert(n == ys.size.toUInt())
        return (0u until m).map { r ->
            (0u until n).toList()
                .sumOf { k -> get(r, k) * ys[k.toInt()] }
        }.toDoubleArray()
    }

    fun argmax(r0 :UInt, c :UInt, f :(Double) -> Double) :Pair<UInt, Double> {
        var result = r0
        var m = f(get(result, c))
        for (r in r0 + 1u until this.m) {
            val m1 = f(get(r, c))
            if (m < m1) {
                result = r; m = m1
            }
        }
        return Pair(result, m)
    }

    override fun equals(other :Any?) :Boolean {
        if (this === other) return true
        if (other !is RMatrix) return false

        if (n != other.n) return false
        if (m != other.m) return false
        return cs contentEquals other.cs
    }

    override fun hashCode() = 2+ n.hashCode() +31* m.hashCode() +997* cs.contentHashCode()
  }

Der Gaußsche Algorithmus sieht jetzt wie folgt aus:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42


  object RLUFact {
    fun RMatrix.linSolve(ys :DoubleArray) :DoubleArray {
        assert(m>=n)
        val m = copy(pad=1u);  m.paste(0u, n, ys)
        m.gaussElim(n)
        (n until this.m).forEach { xr ->
            assert(abs(m[xr, n])<epsilon)
        }
        return m.backSubst(n)
    }

    private fun RMatrix.backSubst(n :UInt) :DoubleArray {
        for (c in (0u until n).reversed()) {
            if (abd(this[c, c]-1.0)>5*epsilon)
                throw SingularityException("Coefficient Matrix is near singular.")
            for (r in 0u until c) {
                this.add(c, r, -get(r, c))
            }
        }
        val result = (0u until n).map { r -> get(r, n) }
        println(result)
        return result.toDoubleArray()
    }

    private fun RMatrix.gaussElim(n :UInt) {
        var r = 0u
        for (c in 0u until n) {
            val r1 = argmax(r, c) { abs(it) }.first
            swap(r, r1)
            val d = get(r, c)
            if (abs(d)<epsilon) {
                println(this)
                throw SinguarityException("Got down to ${c + 1u} of $n.")
            }
            scale(r, d.inv())
            for (r2 in r+1u until m) {
                add(r, r2, -get(r2, c))
            }
            r++
        }
    }
}

Jetzt ist auch klar, wozu wir einige der Zusatzfunktionen benötigen, argmax liefert die Zeile, in der der betragsgrößte Wert steht, copy(pad :UInt) kopiert die Matrix (wenn man sie verändern will, aber das Original aufheben muss) und fügt zusätzlich leere Spalten hinten an.

Jetzt können wir die Interpolation schreiben:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


  import common.math.RLUFact.linSolve

  data class Interpolate(val xs :DoubleArray, val cs :DoubleArray) :(Double)->Double {
    companion object {
      fun of(xs :DoubleArray, ys :DoubleArray) = Interpolate(xs, createVanDerMonde(xs).linSolve(ys))

      fun createVanDerMonde(xs :DoubleArray) :RMatrix {
        val n = xs.size.toUInt() -1u
        val cs = xs.flatMap { x ->
          var p = 1.0
          listOf(p) +(1u..n).map { p *= x; p }
        }
        return RMatrix(cs.toDoubleArray(), n+1)
      }
    }

    override toString() = cs.toString()

    override fun apply(x :Double) = cs.foldRight(0.0) { c, s -> s*x+c }
  }

Die Berechnung des Polynoms erfolgt nach dem Horner-Schema, d.h. wir berechnen $$ p(x) = c_0+c_1x+c_2x^2+\dots+c_nx^n$$ gemäß der Formel $$ p(x) = (((c_n * x+c_{n-1}) * x+c_{n-2}) * \dots) * x +c_0. $$

Schließlich sollten wir die Interpolation testen, z.B. an der gegebenen Funktion.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


  fun main() {
    val n = 1
    ...
    val domain = DoubleRange(-2.0, 2.0)
    ...
    val f = DescribedFunction("1/(1+x^2)") { x -> 1/(1+x*x) }
    val interpol = DescribedFunction("interpolation", Interpolate.of(xs, f.f(xs)))
    println(interpol)
    val error = DescribedFunction("error") { x -> interpol.f(x)-f.f(x) }
    val window = MyWindow(Plotter(listOf(f, interpol, error), domain))
    ...
  }

Im Bild solltest du 3 Graphen sehen: schwarz die original Funktion ($1/(1+x^2)$), in blau die Interpolation und in grün den Fehler.

Man sieht, dass sich der schwarze und der blaue Graph in 3 Punkten schneiden, nämlich bei $x\in \{-1,0,1\}$. Das ist auch sinnvoll, weil die Interpolation durch diese 3 Punkte gehen sollte. Man sieht weiterhin, dass die Interpolation etwas ähnlich zur original-Funktion ist, d.h. bei $x=0$ geht sie durch $y=1$, danach konkav nach unten. Leider passt die Interpolation außerhalb des Bereiches $(-1,1)$ ziemlich schlecht. Das liegt unter anderem daran, dass das außerhalb des Interpolationsbereiches ist. Man spricht auch von Extrapolation.

Wird das nun besser, wenn man mehr Stützstellen verwendet?

Dazu ändern wir das Hauptprogramm wie folgt ab:

1
2
3
4
5


  fun main() {
    val n = 2
    val xs = (-n..n).map { i -> i.toDouble()*2/n }.toDoubleArray()
    ...
  }

Jetzt schneiden sich die Kurven 5mal, denn wir haben 5 Stützstellen. Außerdem läuft die Interpolation nicht mehr soweit aus dem Ruder. Das liegt daran, dass wir nicht mehr extrapolieren.

Vielleicht können wir den Funktionenplotter noch verbessern, indem wir die Stützpunkte einzeichnen. Das kann man wie folgt erreichen:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


  class Plotter(val fs :List<DescribedFunction>, val domain :DoubleRange, val ps :List<Pair<Double, Double>> =emptyList()) :JComponent() {
    ...
    private fun Graphics.plotCruves() {
      ...
      color = Color.RED
      ps.forEach { (x, y) ->
        fillOval(scale.px(x)-2, scale.py(y)-2, 5,5)
      }
    }
  }

Die Änderung bewirkt, dass die übergebenen Punkte in rot gemalt werden (als kleine Kreise mit Durchmesser 5).

Dazu müssen wir noch das Hauptprogramm anpassen:

1
2
3
4
5
6
7
8
9


  fun main() {
    ...
    val f = Described...
    val ys = f.f(xs)
    val interpol = DescribedFunction("interpolation", Interpolate.of(xs, ys))
    ...
    val window = MyWindow(Plotter(listOf(f, interpol, error), domain, xs.zip(ys)))
    ...
  }

Wenn du das Programm wieder startest, solltest du neben den 3 Kurven noch die 5 roten Punkte sehen, in denen sich die Kurven schneiden.

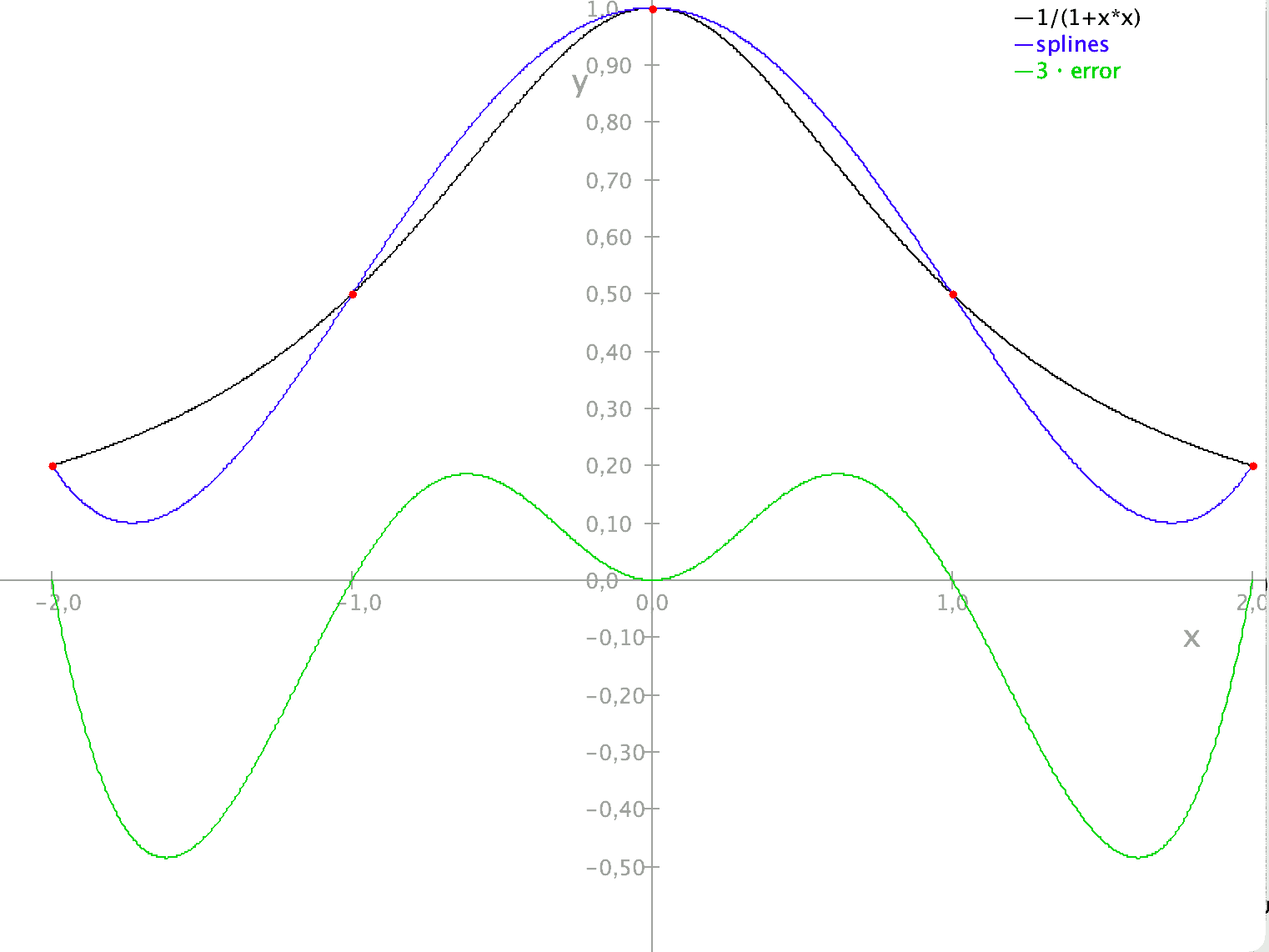Bild 3: Interpolation an 5 Stützstellen. CC Att M. Grützmann 2023.

Wird die Interpolation nun besser, wenn man mehr Stützstellen verwendet?

Im Prinzip ja, aber das sollten wir testen: Dazu im Hauptprogramm folgendes anpassen:

1
2
3
4
5


  fun main() {
    val n = 3
    val xs = (-n..n).map { i -> i.toDouble()*2/n }.toDoubleArray()
    ...
  }

Das sollte zwei Kurven mit 7 Schnittpunkten produzieren (wieder im Bereich $(-2,2)$). Andererseits kommt es bereits zu kleinen Ausbeulungen, so als ob das Polynom nicht ganz an die Originalfunktion ‘ranpasst.

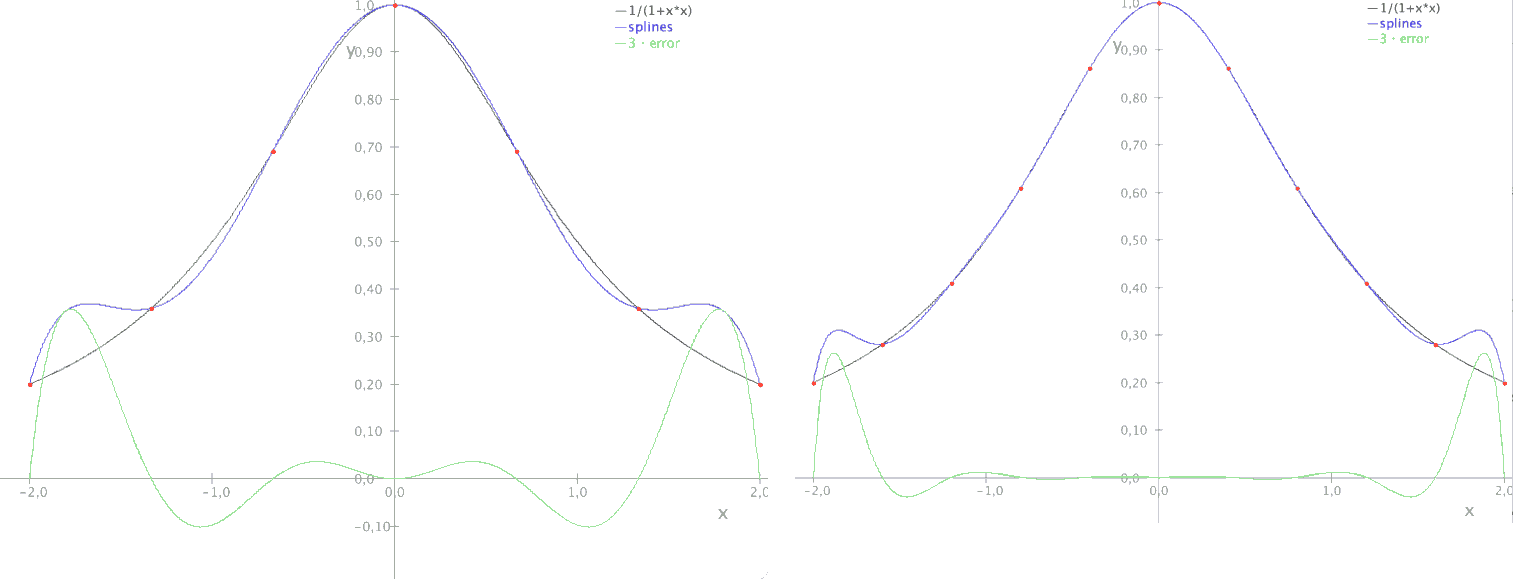Bild 4: Interpolation an 7 und an 11 Stützstellen. Die Fehler in der Mitte werden kleiner, aber der Fehler an den Rändern ändert sich wenig. CC Att M. Grützmann 2023.

Um auch quantitativ zu erkennen, wie gut die Interpolation ist, können wir die Wurzel aus der mittleren quadratischen Abweichung berechnen (RMSE), etwa wie folgt:

1
2


  fun rmse(error: DescribedFunction, domain :DoubleRange, n :UInt =1000u) = sqrt(error.f(domain.partitition(n))
      .sumOf { x -> x*x }/n.toInt())

Die muss man dann im Hauptprogramm aufrufen, um das Ergebnis zu sehen:

1
2
3
4
5
6
7


  fun main() {
    ...
    val error = DescribedFunction(...)
    val rmse = rmse(error, domain)
    println("Der mittlere Fehler bei der Interpolation beträgt $rmse.")
    val window = ...
  }

Wenn du das Programm neu startest, dann sollte in der Konsole als letzte Zeile der “mittlere Fehler der Interpolation” ausgegeben werden. Der Wert ist wahrscheinlich etwa so groß, wie die größte Abweichung an den Rändern. Wenn du das Programm für verschiedene Anzahl Stützstellen ausführst, sollte der RMSE tendentiell kleiner werden.

Wenn du jetzt n weiter erhöhst, können 2 Dinge passieren: Es funktioniert und du erhältst mehr Schnittpunkte. Oder es gibt Rechenfehler, die zu schlechteren Approximationen führen oder schließlich sogar zum Versagen der Berechnung der Interpolation (SingularityException).

4. Eine Idee von Bézier und Casteljau

Die Interpolation hat 3 Probleme:

Zum einen wird die Berechnung immer komplexer (die van der Monde Matrix wird immer größer);
Es treten immer größere Rechenfehler auf;
Die Polynome können leicht überschwingen, also große Abweichungen produzieren, obwohl die Stützpunkte immer dichter zusammen rücken.

Stattdessen hatten Pierre Bézier und Paul de Casteljau in den 1960ern eine andere Idee. Statt 1 Polynom zu verwenden, verwendeten sie eine Reihe von Polynomen, die jeweils in einem Interval zwischen benachbarten Stützstellen gelten. Damit das ganze eine glatte Kurve ergibt, verlangten sie, dass an den Übergangsstellen nicht nur der vorgegebene Funktionswert eingehalten wurde (die Kurve stetig war), sodern auch die 1. und die 2. Ableitung stetig sein sollte.

Wenn man $n+1$ Stützpunkte hat, gibt es $n$ Intervalle, und in jedem dieser Intervalle ein Polynom von Grad 3 (sodass an beiden Enden die 2. Ableitung verschieden sein kann). Man hat also $4n$ unbekannte Koeffizienten und fordert $4n-3$ Bedingungen:

$$\begin{array}{rl} b^3_0(x_0) &= y_0, \\ b^3_0(x_1) &= y_1, \\ b^\prime_0(x_1) &= b^\prime_1(x_1), \\ b^\prime{}^\prime_0(x_1) &= b^\prime{}^\prime_1(x_1), \\\hline b^3_1(x_1) &= y_1, \\ b^3_1(x_2) &= y_2, \\ b^\prime_1(x_2) &= b^\prime_2(x_2), \\ b^\prime{}^\prime_1(x_2) &= b^\prime{}^\prime_2(x_2), \\\hline &\vdots \\ b^3_{n-1}(x_n) &= y_n. \end{array}$$

Dazu müsste man jetzt fleißig sein und aus $b^3_i(x)= a_{i,0}+a_{i,1}x+a_{i,2}x^2+a_{i,3}x^3$ die Ableitung ausrechnen und dann das entsprechende Gleichungssystem aufstellen. Aber selbst wenn man das alles fehlerfrei macht, wird das Gleichungssystem am Ende keine eindeutige Lösung haben, weil es eben $4n$ Koeffizienten aber nur $4n-3$ Gleichungen sind.

Stattdessen hatte Bézier eine bessere Idee, wie man das Gleichungssystem systematisch aufschreiben kann: Wir definieren der Reihe nach Interpolationsfunktionen für den Grad 0, 1, 2 und 3 wie folgt:

$$ b^0_i(x) = \theta(x-x_i) -\theta(x-x_{i+1}) = \begin{cases} 1&\text{für } x_i\le x< x_{i+1},\\ 0&\text{sonst.} \end{cases} $$ $$ b^k_i(x) = \omega^k _ i(x)b^{k-1} _ i(x) +\left(1-\omega^k _ {i+1}(x)\right)b^{k-1} _ {i+1}(x) $$ $$\text{mit}\quad\omega^k_i(x) = \begin{cases} \frac{x-x_i}{x_{i+k}-x_i} &\text{für } x_i\ne x_{i+k}, \\ 0&\text{sonst.} \end{cases} $$

Die Funktionen $b^k_i(x)$ sind stückweise $k$-fach stetig, also $b^0_i(x)$ stückweise stetig (und stückweise konstant), $b^1_i(x)$ stückweise stetig differenzierbar, $b^2_i(x)$ stückweise 2-fach stetig differenzierbar und $b^3_i(x)$ stückweise 3-fach stetig differenzierbar. Da $b^k_i(x)$ stückweise $k$-fachs stetig differenzierbar ist, ist es insbesondere $k-1$-fach stetig differenzierbar.

Wenn wir bis zum Grad 3 gehen wollen, dann gibt es $n+4$ solche Funktionen – $\mathbf b^3(x) = (b^3_{-3}(x),b^3 _ {-2}(x),\dots,b^3_n(x))^T$. Diese Funktionen erfüllen aber noch eine Zusatzbedingung $$ \sum_{i=-k}^n b^k_i(x) \equiv 1\text{ für } x_0\le x< x_n. $$

Um diese Funktionen besser zu verstehen, wollen wir sie zunächst plotten. Dazu schreiben wir folgende Klasse:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


  data class Bspline(val xs :DoubleArray, val deg :UByte =3u) {
    companion object {
      fun theta(x :Double) = when {
        x>=0 -> 1.0
        else -> 0.0
      }
    }

    init {
      assert(xs.size>deg.toInt())
    }

    fun DoubleArray.pick(i :Int) = get(min(max(0, i), size-1))

    fun omega(i :Int, k :UByte, x :Double) = when {
      xs.pick(i+k.toInt()) > xs.pick(i) -> (x-xs.pick(i))/(xs.pick(i+k.toInt()) -xs.pick(i))
      else -> 0.0
    }

    fun b(i :Int, k :UByte, x :Double) :Double = when(k.toInt()) {
      0 -> theta(x-xs.pick(i)) -theta(x-xs.pick(i+1))
      else -> omega(i, k, x)*b(i, (k-1u).toUByte(), x) +(1-omega(i+1, k, x))*b(i+1, (k-1u).toUByte(), x)
    }

    fun b(x :Double, k :UByte =deg) = (-k.toInt() until xs.size).map { i -> b(i, k, x) }.toDoubleArray()
  }

Zusammen mit dem Hauptprogramm:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


  fun main() {
    val n = 2
    val xs = (-n..n).map { i -> i.toDouble()/n }.toDoubleArray()
    val domain = DoubleRange(-1.0, 1.0)
    val k = 3.toUByte()
    val splines = Bspline(xs, k)
    val bs = (0 until (splines.b(0.0).size)).map { i ->
      DescribedFunction("b^{k}_${i-k}(x)") { x -> spline.b(x)[i] }
    } + listOf(DescribedFunction("sum") { x -> spline.b(x).sum() })
    val window = MyWindow(Plotter(bs, domain))
    windows.isVisible = true
  }

Dann ergibt sich folgendes Bild:

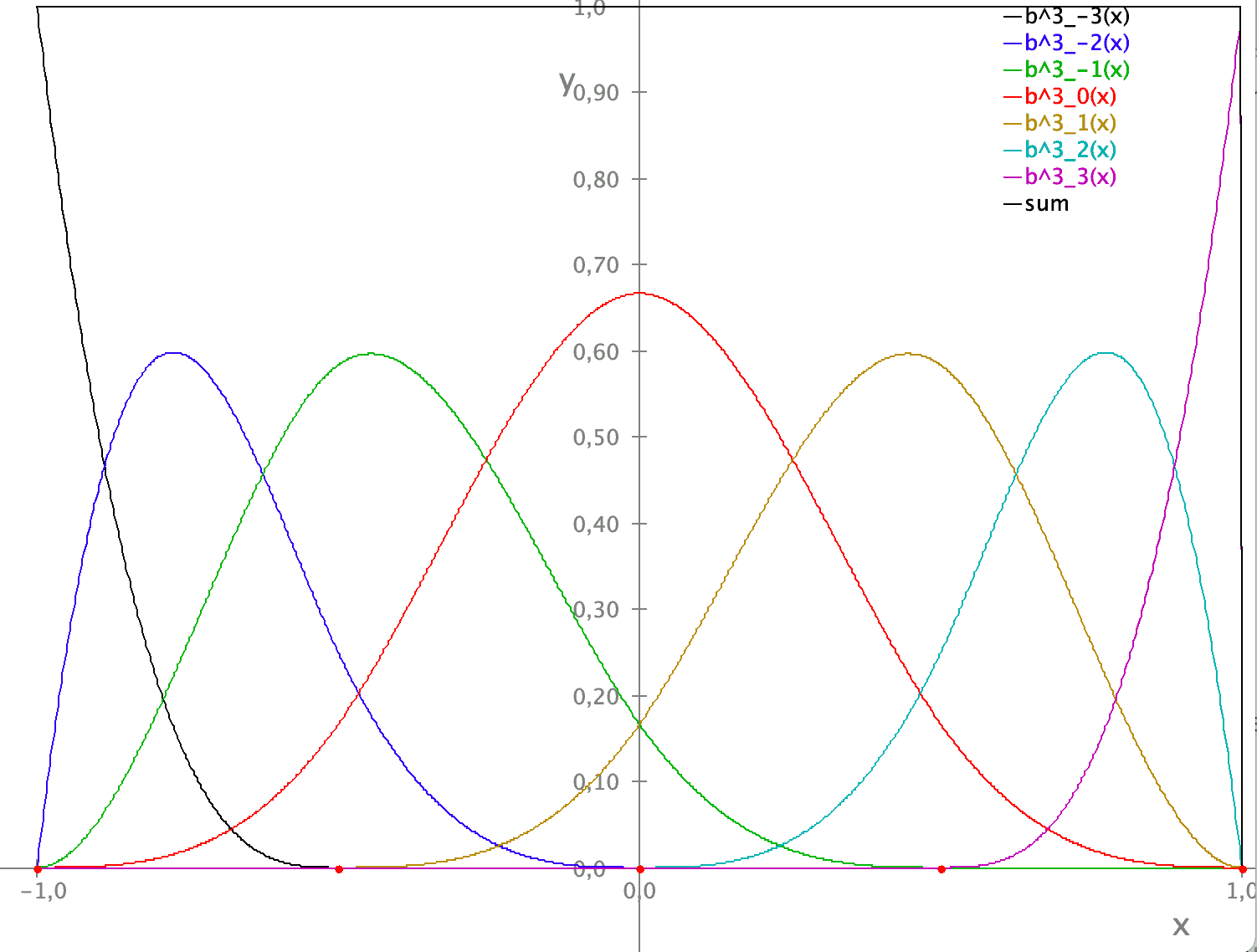Bild 5: Stützfunktionen nach Casteljau. CC Att M. Grützmann 2023.

5. Berechnung der Koeffizienten

Das eigentliche Problem ist die Berechnung der Bézier-Koeffizienten. Dazu entnehmen wir aus [3] folgende Formeln:

$$ f(x) = \mathbf b(x)\cdot \mathbf c,\quad \mathbf c = G^{-1}X\mathbf{y}, $$ $$ G = XX^T,\quad X = (\mathbf b(x_0),\dots,\mathbf b(x_n)). $$

D.h. dass wir ein lineares Gleichungssystem $G\mathbf c= X\mathbf y$ nach den Koeffizienten $\mathbf c$ auflösen müssen. Der Vorteil von diesem Gleichungssystem ist, dass die Koeffizientenmatrix $G$ symmetrisch und positiv semi-definit ist.

Wir können zunächst versuchen, dass Gleichungssystem mit dem Gauß-Algorithmus zu lösen. Dazu implementieren wir also folgende zusätzlichen Funktionen:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


  import common.math.LUFact.linSolve

  data class Bspline(val xs :...) {
    ...

    fun b() = Matrix(xs.flatMap { x -> b(x) }.toDoubleArray(), b(0.0).size.toUInt()).transpose()

    fun fit(ys :DoubleArray) :Fit {
      assert (xs.size==ys.size)
      val x = b();  println(x);  println()
      val xy = x.times(ys)
      val g = x.timesT(x);  println(g);  println()
      return Fit(this, g.linSolve(xy))
    }
  }

  data class Fit(s :Bspline, cs :DoubleArray) :(Double)->Double {
    val xs = s.xs

    override fun invoke(x :Dobule) = s.b(x).dot(cs)
  }

    data class RMatrix(...) {
      ...
      fun timesT(f :RMatrix) :RMatrix {
          assert(n == f.n)
          return Matrix((0u until m).map { r ->
              (0u until f.m).map { c ->
                  (0u until n).sumOf { k -> get(r, k) * ys[k.toInt()] }
              }
          }.toDoubleArray(), f.m)
      }
    }

Die Matrix-Multiplikation fun timesT(f :RMatrix) berechnet das Produkt 2er Matrizen. Im Unterschied zu operator fun times(f :RMatrix) geht aber die 2. Matrix transponiert ein.

Diese Funktionen ruft man wie folgt auf:

1
2
3
4
5
6
7
8
9


  fun main() {
    ...
    val f = DescribedFunction("1/(1+x^2)") { x -> 1/(1+x*x) }
    val ys = f.f(xs)
    val fit = DescribedFunction("spline", splines.fit(ys))
    val error = DescribedFunction("error") { x -> fit.f(x) -f.f(x) }
    val window = MyWindow(Plotter(listOf(f, fit, error), domain, xs.zip(ys)))
    window.isVisible = true
  }

Leider funktioniert das nicht, sondern stürzt mit SingularityException ab. Dafür gibt es 2 Gründe: Zum einen ist das Gleichungssystem unterbestimmt. Aus der Fehlermeldung sieht man, dass der Löser bis zur Zeile “5 von 7” kommt, d.h. dass 2 Koeffizienten überflüssig sind und wir entsprechend 2 Stützfunktionen weglassen sollten. Zum anderen kann es gut sein, dass der Gaußsche Algorithmus nicht die stabilste Methode ist, das Gleichungssystem zu lösen.

Ein Blick auf Bild 5 zeigt, dass wir zwar die Funktionen $b^3 _ {-3}(x)$ und $b^3_3(x)$ brauchen (um den Anfangs- und Endpunkt zu erreichen), aber $b^3 _ {-2}(x)$ und $b^3_2(x)$ ihr Maximum zwischen zwei Stützstellen haben. Deshalb lassen wir die einfach weg. Dazu modifizieren wir die Methoden fun b(x :Double, k :UByte =deg) und fun b() :Matrix wie folgt:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


  fun b(x :Double, k :UByte =deg) :DoubleArray {
    val indices = when (k.toInt()) {
      1 -> 0 until xs.size-2
      2 -> 0 until xs.size -2
      3 -> -1 until xs.size -3
      else -> TODO("unimplemented")
    }
    val cs = listOf(b(-k.toInt(), k, x)) + indices.map { i -> b(i, k, x) } +listOf(b(xs.size-2, k, x))
    return cs.toDoubleArray()
  }

  fun b() :Matrix {
    val n = xs.size-2
    val cs = xs.subList(0, xs.size-1).flatMap { x -> b(x) } +(DoubleArray(n-1){0.0}.toList()+listOf(1.0))
    return Matrix(cs.toDoubleArray(), n).transpose()
  }

Der Grund für die Modifikation von fun b() :Matrix ist, dass die Funktionen b(x) am rechten Rand alle bereits 0 werden, wir aber in der letzten Spalte der Matrix die Summe 1 brauchen.

Damit und mit dem letzten Hauptprogramm sollte es jetzt erst einmal klappen, d.h. du erhältst ein Ergebnis ähnlich zu Bild 2.

9. Selber Experimentieren

Jetzt ist Zeit, das Programm ausgiebig zu testen. Dazu kannst du sowohl die Zielfunktion ändern als auch die Anzahl der Stützstellen, oder sogar einfach ein paar Funktionswerte vorgeben.

Vielleicht kannst du dich mit oszillierenden Funktionen probieren: Das typische Beispiel ist die Sinus-Funktion fun sin(x :Double) :Double, die du aus dem Paket “kotlin.math” importieren kannst. Die Funktion beginnt bei $\sin 0 = 0$ und wiederholt sich alle $2\pi\approx 6.28$ Die Zahl $\pi$ spricht man pi aus und kann man als Konstante PI ebenfalls aus “kotlin.math” importieren. Du kannst ja damit anfangen, die Funktion zwischen 0 und $2\pi$ mit 5 Stützstellen zu interpolieren (entweder exakt oder mit Bézierkurven). Dann könntest du auch einfach $4n+1$ Stützpunkte vorgeben, nach dem Prinzip val xs = (0..4*n).map { k -> PI*k/2 }.toDoubleArray() und val ys = doubleArrayOf(0.0,1.0,0.0,-1.0, 0.0,1.0,0.0,-1.0, ..., 0.0) und schauen, wir gut die Interpolation klappt. Bevor zu aber 13 Stützpunkte angibst, solltest du es erst einmal mit 5 Stützpunkten probieren. Der Grund ist, dass der Gaußsche Algorithmus nicht beliebig genau ist, die Bézierkurven eventuell instabil werden.

9.2 Numerische Bibliothek Verwenden

Wenn du die Interpolation/Bézierkurven weiter treiben willst, könntest du versuchen, eine numerische Bibliothek zum Lösen des linearen Gleichungssystems zu verwenden. Dazu müsstest du die “build.gradle.kts” zunächst anpassen. Eine interessante Bibliothek, die in der JVM funktioniert, wäre “org.ojalgo:ojalgo”, die zum Zeitpunkt des Schreibens in der Version “52.0.1” vorliegt. Dazu müsstest du die Datei “build.gradle.kts” im Hauptordner des Programms wie folgt anpassen:

1
2
3
4


dependencies {
    implementation("org.ojalgo:ojalgo:52.0.1")
    testImplementation(kotlin("test"))
}

d.h., wenn es den Block dependencies {...} schon gibt, solltest du schauen, dass er dann auch die Zeile implementation("org....") enthält. Falls es den Block noch nicht gibt, kannst du den gesamten Inhalt irgendwo zwischen den anderen Blöcken anlegen (nicht zu weit vorne). Eventuell musst du auch den Block

1
2
3


tasks.test {
    useJUnitPlatform()
}

noch ergänzen. Danach musst du die Datei neu importieren. Dazu sollte nach dem Bearbeiten ein Symbol mit grauem Hintergrund, einem dunkelgrauen Elefant und 2 blauen Pfeilen, die im Kreis zeigen, auftauchen. Entweder klickst du auf dieses Symbol (wenn du es siehst) oder du öffnest den “Gradle”-Reiter (am rechten oberen Rand) und klickst dort links-oben auf die 2 grauen Pfeile, die im Kreis zeigen. Nach kurzem Import sollte das erste Symbol verschwinden.

Du musst dann entsprechend die 4 Methoden fun b(x :Double, k :UByte =deg), fun b() :Matrix, fun fit(ys :DoubleArray) :Fit in Bspline und fun Fit::apply(x :Double) :Double anpassen, etwa wie folgt:

Die Klasse Fit muss auf Vektoren aus der Bibliothek umgestellt werden:

1
2
3
4
5


  data class Fit(private val s :Bspline, val cs :MatrixStore<Double>) :(Double)->Double {
        val xs = s.xs

        override fun invoke(x :Double) :Double = cs.multiply(s.b(x))[0,0]
  }

Die Methode fun fit(ys :DoubleArray) :Fit ändert sich wie folgt:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


  import org.ojalgo.matrix.store.Primitive64Store
  ...

  data class Bspline(val xs :DoubleArray, val deg :UByte =2u) {

    companion object {
      fun theta(...) ...

      val mFactory = Primitive64Store.FACTORY
    }

    ...

    fun fit(ys :DoubleArray) :Fit {
      assert(xs.size==ys.size)
      val x = b();  println(x);  println()
      val xy = x.multiply(mFactory.column(*ys))
      val g :MatrixStore<Double> = x.multiply(x.transpose())
      println(g);  println()
      val solver = Cholesky.PRIMITIVE.make(g)
      val ok = solver.checkAndDecompose(g)
      assert(ok)
      println(solver.l)
      assert(solver.isSolvable)
      return Fit(this, solver.solve(xy).get().transpose())
    }
  }

D.h. dass wir für die symmetrische Matrix g eine Cholesky-Faktorisierung verwenden. Deren Berechnung ist numerisch stabiler als der Gaußsche Algorithmus. Wichtig ist, dass man g zweimal übergeben muss, einmal an .make() und einmal an .checkAndDecompose(). Beim ersten Aufruf wird lediglich genug Speicher für die Operation initialisiert und die Cholesky-Klasse initialisiert. Erst beim zweiten Aufruf wird die eigentliche Faktorisierung durchgeführt. Man beachte auch, dass man nach der Methode .solve(xy) noch ein .get() aufrufen muss, da man sonst nicht das Ergebnis erhält. Die Regeln für Matrizenmultiplikation verlangen, dass wir die Koeffizienten als Zeilenmatrix verwenden müssen, also noch einmal transponieren müssen.

Schließlich müssen wir auch die beiden Methoden b(...) anpassen, damit die mit den restlichen Methoden zusammen arbeiten:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


  fun b(x :Double, k :UByte =deg) :Primitive64Store {
    val indices = when (k.toInt()) {
        1 -> 0 until xs.size-2
        2 -> 0 until xs.size -2
        3 -> -1 until xs.size -3
        else -> TODO("unimplemented")
    }
    return mFactory.column(*(listOf(b(-k.toInt(), k, x)) +
            indices.map { i -> b(i, k, x) } + listOf(b(xs.size-2, k, x)) ).toDoubleArray())
  }

  internal fun b() :MatrixStore<Double> {
    val cols = xs.slice(0 until xs.size-1).map { x -> b(x) } +
            listOf(mFactory.column(*(Array(xs.size-1) { 0.0 }.toList() + listOf(1.0)).toDoubleArray()))
    return mFactory.columns(*cols.toTypedArray())
  }

Konkret heißt die obige Definition von fun b(x :Double, ...), dass wir nur mit Splines vom Grad 1, 2 oder 3 arbeiten können, aber das sind die häufigsten Grade. In den obigen Beispielen hatten wir ja stets Grad 3 verwendet.

Viel Erfolg beim Probieren.

9.3 Weiterführende Ideen

Wie man bereits am Titel von [3] sieht, ist eine der neueren Entwicklungen zu Bézierkurven das automatische Wählen weiterer Stützstellen. Wie wir bereits bei der Interpolation gesehen hatten, weicht die Näherung an manchen Stellen stärker von der exakten Kurve ab, als an anderen Stellen. Die Idee ist nun, die Punkte nicht mehr äquidistant zu wählen, sondern an den Stellen dichter zu setzen, wo die Abweichung größer war. Dazu muss man aber die Originalkurve gut berechnen können.

Eine Alternative ist es, die Splines so zu wählen, dass die Krümmung nicht allzu groß wird. Das kann man erreichen, indem man nicht einfach das Gleichungssystem löst, sondern eine Optimierungsaufgabe, bei der man etwa folgende Verlustfunktion verwendet (Verlust=schlecht => Minimieren, s.a. [3]): $$ L[f; N] = \sum_{i=0}^N \left(f(x_i)-p(x_i)\right)^2 +\lambda\frac1{b-a}\int_a^b \left(p’’(x)\right)^2\,dx. $$

Dabei ist $\lambda\ge0$ der Gewichtungsparameter. Für $\lambda=0$ erhält man das klassische Bézier-Interpolations-Problem. Für $\lambda>0$ wird starke Krümmung bestraft.

9.9 Zusammenfassung

Inzwischen hast du vielleicht festgestellt, dass die Programme länger werden und mehr probiert werden muss, bevor etwas schön funktioniert. Das ist die Realität beim Programmieren. Am obigen Beispiel habe ich ca. 2 Wochen gefeilt, bis es halbwegs funktioniert hat. Zum Nachprogrammieren (anhand der Hinweise im Text) brauchst du vielleicht 1–3 Wochenenden. Sei also nicht verzagt, wenn es nicht an 1 Wochenende klappt.

Prinzipiell gilt für Projekte, dass man sich überlegen sollte, was das langfristige Ziel ist, welche prinzipiellen Schritte man dafür braucht, welches zusätzliche Wissen/ welche Literatur und in welchen Etappen / mit welchen Zwischenerfolgen man vorgehen möchte. Es empfiehlt sich, einfache erste Zwischenziele zu setzen (und diese dann langsam zu steigern), damit man den Mut nicht verliert. Auch wenn man ein Projekt nicht (gleich) bis zum Abschluss bringt, lernt man beim Durchführen solcher Projekte oft viel mehr, als wenn man nur beliebige Texte über das Programmieren lesen würde.

Für diejenigen, die als Oberschüler bereits mit Projekten zurechtkommen, gibt es Jugend Forscht, bei dem man abgesteckte kleine Projekte selbst durchführen kann, zum Beispiel in Mathematik, Informatik oder anderen Natur- und Ingenieurwissenschaftlichen Gebieten. Motivierender ist es auch, wenn man ein Projekt mit 1 oder 2 interessierten Freunden gemeinsam durchführt und sich gegenseitig regelmäßig motiviert, weiter zu kommen und die Zwischenergebnisse anzusehen.

Weiterführende Literatur