Nachdem wir letztes Mal über fälschungssichere Übertragung und Kryptographie gesprochen haben, wollen wir heute über störungssichere Übertragung sprechen.

1. Bilder von den Voyager-Sonden

Zunächst sollten wir klären, wo man das einsetzen kann. Also die Voyager-Sonden wurden vor 75 Jahren in Richtung Neptun und jenseits des Sonnensystems losgeschickt, um Erkundungen des Weltraums auch dort zu ermöglichen. Zum einen hatten die Sonden ein paar Aufzeichnungen von der Menschheit auf der Erde (in den 1970ern) mit und zum anderen sind Kameras und starke Sendeanlagen in den Sonden eingebaut. Mithilfe von Solarkollektoren und radionukleid-Batterien erhalten die Sonden Strom, um Signale zu Erde zurück zu senden. Das Problem ist aber, dass aufgrund der großen Entfernungen und auch aufgrund von Sonnenstürmen, diese Signale meist nicht fehlerfrei auf der Erde ankommen.

Wenn man sich an das Rauschen von UKW- und Mittelwellenradio erinnert, dann kann das selbst für die Kommunikation innerhalb eines Kontinents ein Problem werden. Eine Verbesserung wurde bereits mit digitalen Signalen erreicht, d.h. hier ist nicht mehr die Frage, ob das Signal, welches um Größenordnungen geringer ist und von Rauschen übertönt, nun halb- oder viertel so groß ist, sondern lediglich, ob die ankommende Schwingung 0 oder 1 codiert. Dadurch kann man auch bei mittelschlechtem Signal-Rausch-Verhältnis die Informationen noch gut entnehmen. Was aber, wenn selbst das digitale Signal durch Rauschen verfälfscht wird?

Eine vergleichbare Situation liegt bei der Langzeitspeicherung von Computerdaten vor. Früher wurden die auf Magnetbänder gespeichert, die ebenfalls eine Folge von 0en und 1en kodierten. Zwischendurch verwendete man magnetische Festplatten, heute werden flash-ROMs verwendet. Gemeinsam ist, dass eine Folge von 0en und 1en gespeichtert ist und man zum einen verifizieren sollte, dass die nicht gestört wurde, also Rauschen enthalten ist, und zum anderen, falls Rauschen enthalten ist, schauen, ob und wie man das Original-Signal rekonstruieren kann.

2. Eine Einfache Idee

Wenn man nicht sicher ist, ob ein Signal 100% fehlerfrei übertragen wird, dann kann man das gleiche Signal einfach 2-mal übertragen und anschließend vergleichen, ob das Ergebnis übereinstimmt. Leider verdoppelt man damit die Länge der übertragenen Nachricht.

Wenn man außerdem im Falle leichter Fehler auch noch das korrekte Signal wiedergewinnen will, kann man das ursprüngliche Signal 3-mal übertragen und dann schauen, ob 1) alle 3 Versionen gleich sind (nur dann wurde vollkommen fehlerfrei übertragen) und 2) bei 1 abweichenden Versionen das Mehrheitssignal verwenden. Das ganze gibt natürlich nur Sinn, wenn man digitale Signale verwendet, da bei Analogen Signalen warscheinlich 3 verschiedene Versionen ankommen werden und den Mittelwert zu bilden, die Fehler nur auf ca. $1/\sqrt3$ reduziert. Leider hat man hierfür das Signal 3-mal so lang gemacht, was für Sonden mit geringer verfügbarer Energie ein Problem sein kann.

Bleibt die Frage, ob man das auch effizienter hinbekommt.

3. Reed-Solomon-Kodierung

Hierzu hatten I.S. Reed und G. Solomon eine zündende Idee aus dem Bereich der Algebra. Das Grundprinzip ist zunächst, dass man nicht einzelne bits/Bytes oder ganze Zahlen verschlüsselt, sondern gleich Gruppen von $d+1$ Zahlen. Wenn jetzt $d=5$ und wir statt 6 Zahlen, 8 Zahlen übermitteln, dann ist das Signal nur um 30% länger geworden, aber mit dem richtigen Verfahren kann man sowohl auf Übertragungsfehler testen als auch einfache Fehler korrigieren.

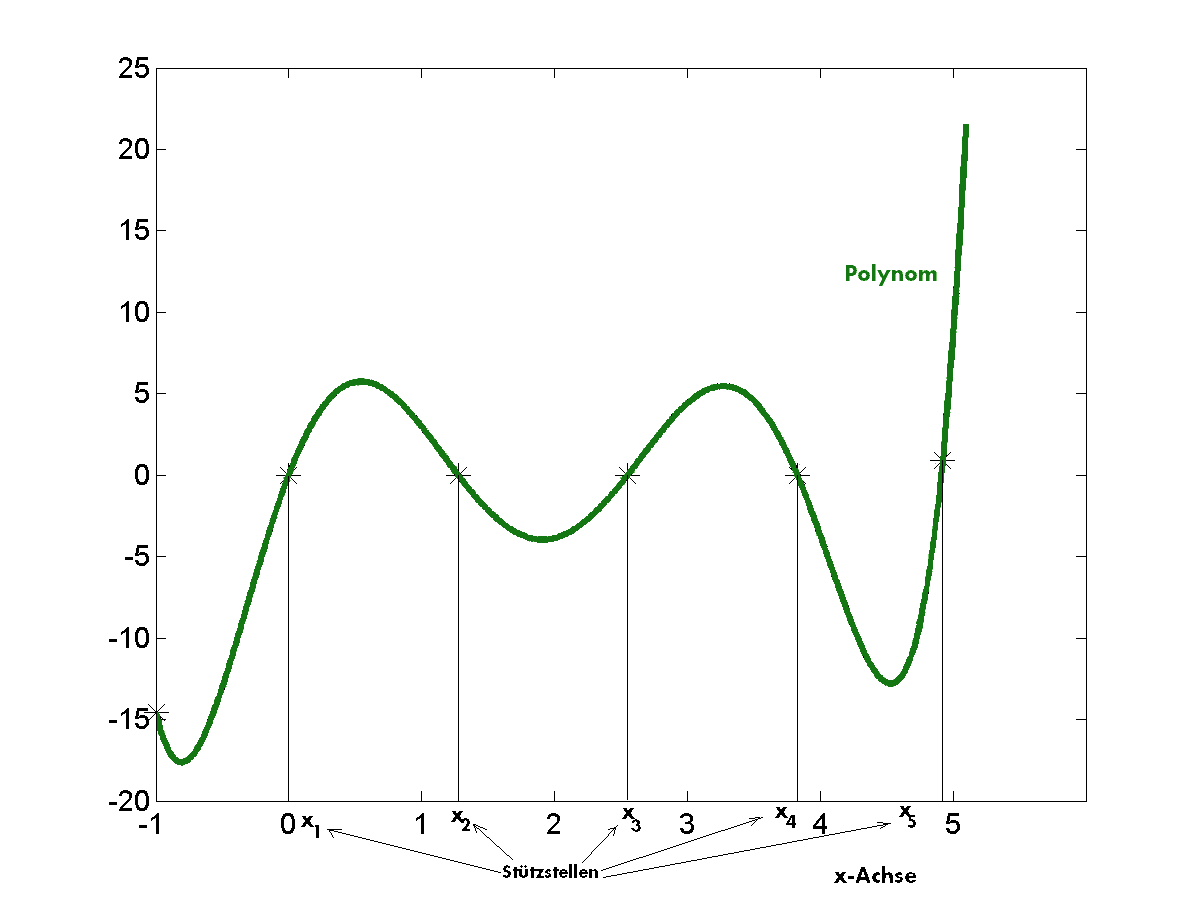
Bild 1: Interpolation, Polynom, das durch Stützpunkte geht.

Das Prinzip ist folgendes: Man kann die $d+1$ Zahlen als die Koeffizienten eines Polynoms (in 1 Variable) vom Grad $d$ schreiben. Aber wie kann man dieses Polynom übertragen? Dazu überlegt man sich, dass ein Polynom $y=p(x)= a_0+a_1x+a_2x^2+\dotsm+a_dx^d$ durch $d+1$ Punkte in der Ebene eindeutig bestimmt ist. Dabei müssen nur die $x$-Koordinaten der Punkte verschieden sein. Wenn man statt $d+1$ Punkten sogar $d+2$ Punkte verwendet, hat man 1 zusätzliche Gleichung zur Kontrolle. Wenn man schließlich $d+3$ Punkte verwendet, kann man probieren, ob davon $d+2$ Punkte auf einem Polynom vom Grad $d$ liegen. Dieses ist dann das richtige Polynom und falls genau 1 Punkt vom Polynom abweicht, weiß man dass wahrscheinlich nur 1 Übertragungsfehler vorkam.

Also was muss man jetzt übertragen?

Wir einigen uns zunächst auf $d+3$ Stützstellen, also die $x$-Werte der Punkte. Dann übertragen wir die Werte $y_k:=p(x_k)$ für diese $0\le k\le d+2$ Stützstellen, also $d+3$ Werte um $d+1$ Koeffizienten zu verschlüsseln.

3.1 Wie sieht das in einem Algorithmus aus?

Dazu nimmt man einfach die Stützstellen $0, 1, -1, 2, -2, 3, -3, \dots$ und bildet das lineare Gleichungssystem:

$$\begin{array}{ccccc} a_0 &+0a_1 &+0a_2 &+\dots &+0a_d &= y_0 \\ a_0 &+1a_1 &+1a_2 &+\dots &+1a_d &= y_1 \\ a_0 &-1a_1 &+1a_2 &-+\dots &+(-1)^da_d &= y_{-1} \\ \dots \\ a_0 &\pm ka_1 &+k^2a_2 &-+\dots &+(\mp k)^da_d &= y_{\mp k} \end{array}$$

Um zu sehen, dass dieses Gleichungssystem immer eine eindeutige Lösung hat, kann man zeigen, dass die Koeffizientenmatrix $$ \left(\begin{array}{ccccc} 1 & x_0 & x_0^2 & \dots & x_0^d \\ 1 & x_1 & x_1^2 & \dots & x_1^d \\ 1 & x_2 & x_2^2 & \dots & x_2^d \\ \vdots \\ 1 & x_d & x_d^2 & \dots & x_d^d \end{array}\right) $$ invertierbar ist, z.B. indem man zeigt, dass die Determinante $\prod_{i<j} (x_j-x_i)\ne0$ ist, solange die Stützstellen verschieden sind.

Wenn du wissen willst, wie man ein solches Gleichungssystem löst, solltest du dich an den Unterricht der 11./12. Klasse halten. Prinzipiell gibt es verschiedene Verfahren, besonders, wenn man nicht zu viele unbekannte Koeffizienten hat. Man kann mit den leichteren Gleichungen anfangen, z.B. $a_0=y_0$ und dieses Ergebnis in die anderen Gleichungen einsetzen, um dann weiter $a_1, a_2, \dots$ zu bestimmen. Oder man kann geeignete Vielfache einer Gleichung von den anderen abziehen, sodass man nur noch $d$ Gleichungen mit $d$ Unbekannten hat und dann entsprechend weiter verfahren. Oder man kann auch 2 Gleichungen nach 1 Variablen auflösen und die Terme gleichsetzen.

Ein systematischer Weg ist das Gauss-Verfahren. Man schreibt die Koeffizienten der $d+1$ Gleichungen und ihre rechten Seiten in eine Matrix und macht dann Zeilenumformungen nach folgendem Schema:

1. Zeilen vertauschen – dabei ändert sich zwar die Reihenfolge der Gleichungen, nicht aber die Lösung für die Koeffizienten,

2. eine Zeile mit eine Zahl ungleich 0 multiplizieren – dabei ändert sich zwar diese Zeile, aber nicht die Lösung (man könnte ja die Zeile wieder durch diese Zahl dividieren),

3. Das Vielfache einer Zeile zu einer anderen Zeile addieren (Gauss Eliminierung) – wenn die 2 Gleichungen vorher gegolten haben, dann gelten die 2 Gleichungen jetzt immer noch.

Die Frage ist noch, wie man das systematisch macht, damit man die Lösungen am Ende ablesen kann:

Zunächst tauschen wir die Zeile mit dem betragsgrößten Koeffizienten von $a_0$ nach oben und dividieren diese Zeile durch diesen Koeffizienten. Dadurch erreichen wir, dass die 1. Zeile mit $1$ beginnt. Jetzt multiplizieren wir diese 1. Zeile der Reihe nach mit den restlichen Koeffizienten von $a_0$ und ziehen sie von der entsprechdenen Zeile ab. Dadurch erreichen wir folgende Struktur:

$$\left(\begin{array}{cccc|c} 1 & * & * & \dots & * \\ 0 & * & * & \dots & * \\ 0 & * & * & \dots & * \\ \vdots \\ 0 & * & * & \dots & * \end{array}\right)$$

Warum ist das besser?

Weil wir in den Zeilen $2\dots d+1$ jetzt nur noch $d$ Variablen haben und wenn wir diese kennen, aus der 1. Zeile $a_0$ berechnen können.

Jetzt verfahren wir mit den Zeilen $2\dots d+1$ ab der Spalte 2 entsprechend und erreichen:

$$\left(\begin{array}{ccccc|c} 1 & * & * & * & \dots & * \\ 0 & 1 & * & * & \dots & * \\ 0 & 0 & * & * & \dots & * \\ \vdots&*& & & \dots & * \\ 0 & 0 & * & * & \dots & * \end{array}\right) $$

Entsprechend verfahren wir mit den Zeilen $3\dots d+1$ ab Spalte $3$ und so weiter, bis wir die Matrix auf obere Dreiecksgestalt gebracht haben:

$$\left(\begin{array}{ccccc|c} 1 & * & * & * & \dots & * \\ 0 & 1 & * & * & \dots & * \\ 0 & 0 & 1 & * & \dots & * \\ \vdots&& & \ddots & \dots & * \\ 0 & \dots&& & 1 & * \end{array}\right) $$

Jetzt kann man aus der unteren Zeile den Koeffizient $a_d= * $ ablesen. Entsprechend kann man diese Koeffizienten rückwärts von den restlichen Gleichungen abziehen, also die letzte Zeile mit den Koeffizienten der letzten Spalte (vor dem $|$) multiplizieren und von der jeweiligen Zeile abziehen. Nacheinander erhält man dabei die Schritte:

$$\left(\begin{array}{ccccccc|c} 1 & * & * & & \dots && 0 & * \\ 0 & 1 & * & & \dots && 0 & * \\ \vdots& &\ddots&*&\dots& * & 0 & * \\ 0 & \dots & & & & 0 & 1 & * \end{array}\right) $$

$$\left(\begin{array}{ccccccc|c} 1 & * & * & & \dots&0& 0 & * \\ 0 & 1 & * & & \dots&0& 0 & * \\ \vdots& &\ddots&*&\dots& 1 & 0 & * \\ 0 & \dots & & & & 0 & 1 & * \end{array}\right) $$

$$\left(\begin{array}{cccc|c} 1 & 0 & \dots & 0 & * \\ 0 & 1 & 0 & \vdots & * \\ \vdots& &\ddots& 0 & * \\ 0 & \dots & 0 & 1 & * \end{array}\right) $$

Schließlich kann man aus der Diagonalform der Koeffizientenmatrix die Lösung $a_0, a_1, \ldots, a_d$ ablesen.

Wenn man zusätzliche Punkte hat, kann man der Matrix weitere Zeilen anfügen. Dadurch wird die Diagonale natürlich nicht länger, stattdessen erhält man weitere Zeilen, deren sämtliche Koeffizienten sich auf 0 reduzieren lassen. Wenn für die auch die rechten Seiten (hinter dem $|$) 0 sind, dann ist das konsistent. Wenn allerdings in einer der 2 zusätzlichen Zeilen die rechte Seite nicht 0 ist, dann ist das ein Übertragungsfehler. Wenn es nur 1 ist, dann hat man die konsistenten Zeilen gefunden und die (wahrscheinlich) richtigen Koeffizienten $a_0, a_1, \ldots, a_d$ bestimmt. Wenn mehr als 1 Zeile inkonsistent ist, dann hat man eine falsche Zeile verwendet und muss noch einmal von vorn beginnen. Jetzt bleibt nur hartnäckiges Probieren, man muss jeweils 1 der oberen Zeilen weglassen und schauen, ob das restliche System sich konsistent lösen lässt. Wenn man eine solche Kombination gefunden hat, dann hat man die Übertragung noch entschlüsselt.

In einem Kotlin-Programm sieht das wie folgt aus: Zunächst sollten wir Matritzen definieren:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78

  data class Matrix(private val cs :DoubleArray, val n :UShort) {

    val m = cs.size/n

    init {
      assert (m*n == cs.size.toUInt())
    }

    fun clone() = Matrix(cs.clone(), n)

    fun toList() = cs.toList()

    override fun toString() = "("+ (0 until m).map { r ->
      (r*n until (r+1)*n).map { off -> cs[off] }.joinToString()
    }.joinToString(")\n(") +")"

    fun slice(rRange :UIntRange, cRange :UIntRange) :Matrix {
      val n1 = cRange.last-cRange.fist+1u
      val r0 = rRange.first;  val c0 = cRange.first
      val ncs = DoubleArray(((rRange.max-rRange.min+1u) * n1).toInt())
      var offset0 = -c0.toInt()
      var offset = (r * n).toInt()
      for (r in rRange)
        for (c in cRange) {
          ncs[offset0 +c.toInt()] = cs[offset +c.toInt()]
          offset0 += n1.toInt()
          offset += n.toInt()
        }
      return Matrix(ncs, n1)
    }

    operator fun get(r :UInt, c :UInt) = cs[r.toInt()*n.toInt() +c.toInt()]

    operator fun set(r :UInt, c :UInt, value :Double) {
      cs[(r*n +c).toInt()] = value
    }

    fun paste(r0 :UInt, c0 :UInt, ys :Matrix, rRange :UIntRange, cRange :UIntRange) {
      assert (r0 +rRange.last-rRange.first < m)
      assert (c0 +cRange.last-cRange.first < n)
      var offset0 = (r0*n +c0).toInt() -cRange.first.toInt()
      var offset = (rRange.first * ys.n).toInt()
      for (r in rRange) {
        for (c in cRange)
          cs[offset0 +c1] = ys.cs[offset +c.toInt()]
        offset0 += n.toInt()
        offset += ys.n.toInt()
      }
    }

    fun swap(r :UInt, r0 :UInt) {
      if (r==r0)
        return
      assert (r<m && r0<m)
      val offset = (r*n).toInt()
      val offset0 = (r0*n).toInt()
      for (c in 0 until n.toInt()) {
        val tmp = cs[offset +c]
        cs[offset +c] = cs[offset0 +c]
        cs[offset0 +c] = tmp
      }
    }

    fun scale(r :UInt, f :Double) {
      assert (r<m)
      val offset = (r * n).toInt()
      for (c in 0 until n.toInt())
        cs[offset +c] *= f
    }

    fun add(r0 :UInt, r :UInt, f :Double) {
      assert (r0<n && r<n)
      val offset0 = (r0 * n).toInt()
      val offset = (r * n).toInt()
      for (c in 0 until n.toInt())
        cs[offset +c] += cs[offset0 +c] * f
    }
  }

Dann sollten wir den Lösungsansatz hinschreiben:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

  fun decode(xs :List<Double>, d :UShort, ys :Matrix) :Pair<Matrix, List<Boolean>> {
    assert (xs.size.toUInt() == ys.m)
    val m = createVanDerMonde(xs, d, ys.n)
    m.paste(0, d+1u, ys, 0 until ys.m, 0 until ys.n)
    val result = Matrix(DoubleArray(((d+1u)*ys.n).toInt()), ys.n)
    val solved = (0u until ys.n).map { false }.toMutableList()
    for (swapRow in (0u..(d+1u)).reversed()) {
      m.swap(d+1u, swapRow)
      if (trySolve(result, solved, m,d))
        return Pair(result, solved)
      m.swap(d+1u, swapRow)
      if (swapRow>d)
        continue
      m.swap(d+2u, swapRow)
      if (trySolve(result, solved, m,d))
        return Pair(result, solved)
      m.swap(d+2u, swapRow)
    }
    return Pair(result, solved)
  }

  fun createVanDerMonde(xs :List<Double>, d :UShort, pad :UInt) :Matrix {
    val result = Matrix(DoubleArray(xs.size *(d+1u+pad).toInt()), d+1u +pad)
    xs.forEachIndexed { r, x ->
      var p = 1.0
      for (c in 0u..d.toUInt()) {
        m[r.toUInt(), c] = p
        p *= x
      }
    }
    return result
  }

  fun trySolve(result :Matrix, solved :MutableList<Boolean>, m :Matrix, d :UShort) {
    try {
      val u = gaussEliminate(m, d, true)
      val guess = backSubstitute(u, d)
      for (c in 0u until result.n)  if (!solve[c.toInt()]) {
        if (abs(guess[d+1u, c])<epsilon || abs(guess[d+2u, c])<epsilon) {
          result.copy(0u, c, guess, 0u until d.toUInt(), c..c)
          solved[c.toInt()] = true
        }
      }
      return solved.all { it }
    } catch(e :SingularityException) {
      // fall through
    }
    return false
  }

Die Funktion decode nimmt d+3 Stützstellen (die xs) entgegen sowie $k * (d+3)$ übertragene Werte (die ys). Aus denen berechnet sie die Originalwerte eine $k * (d+1)$ Matrix. Da nicht sicher ist, dass man alle Koeffizienten decodieren kann, gibt die Funktion zusätzlich noch die Liste mit den erfolgreich dekodierten Spalten zurück (ein true in den Spalten, die erfolgreich dekodiert wurden).

Dann brauchen wir noch die 2 Schritte beim Lösen des Gleichungssystems:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

  const val epsilon = 1e-16

  class SingularityException(msg :String ="Singuarity") :Exception(msg) {}

  fun backSubstitute(m :Matrix, d :UShort) :Matrix {
    val m1 = m.clone()
    for (r in (0u..d.toUInt()).reversed()) {
      val f = m[r, r]
      if (abs(f-1.0)>epsilon)
        throw SingularityException("Die Matrix ist (fast) singulär.")
      for (r1 in 0u until r) {
        m1.add(r, r1, -m1[r1, r])
      }
    }
    return m1.slice(0u until m1.m, (d+1u) until m1.n)
  }

  fun gaussEliminate(m :Matrix, d :UShort, limit :Boolean =false) :Matrix {
    val m1 = m.clone()
    var r = 0u
    for (c in 0u..d.toUInt()) {
      val i = argmax(m1, c, if (limit) d.toUInt()  else m1.m){ v -> abs(v) }
      val f = m1[i, c]
      if (abs(f)<epsilon)
        continue
      m1.swap(i, r)
      m1.scale(r, 1/f)
      for (r1 in r+1u until m1.m) {
        m1.add(r, r1, -m1[r1, c])
      }
      r++
      if (r>=m1.m)
        break
    }
    return m1
  }

  fun argmax(m :Matrix, c :UInt, limit :UInt, f :(Double)->Double) :UInt {
    var result = c
    var v = f(m[result, c])
    for (r in c+1u until limit) {
      val v1 = f(m[r, c])
      if (v1>v) {
        result = r;  v = v1
      }
    }
    return result
  }

Die Funktion gaussEliminate hat einen zusätzlichen Parameter limit :Boolean der angibt, ob ein möglicherweise überbestimmtes Gleichungssystem so stabil wie möglich gelöst werden soll (limit=false, d.h. auf alle Zeilen zurückgreifen) oder ob wir zur Eliminierung nur die ersten d Zeilen einsetzen wollen. Wir brauchen das letztere (limit=true), weil wir ja wissen wollen, ob das System aus den ersten d+1 Zeilen lösbar ist und maximal 1 Widerspruch ergibt (in den 2 Kontrollzeilen).

Um das Ganze zu testen, können wir einfache Textnachrichten verschlüsseln:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

  fun main() {
    println("Reed-Solomon Kodierung")
    val d = 3u
    val xs = (1u..(d+3)).map { k -> if (k%2u==0u) -(k/2u).toDouble()  else (k/2u).toDouble() }
    println("Stützstellen: $xs")
    print("  Bitte geben Sie die Nachricht ein: ")
    val msg = readlnOrNull()?.trim() ?: return
    if (msg.isEmpty())
      return
    val dMsg = msg.encodeToByteArray().map { it.toDouble() }
    val k = (dMsg.size.toUInt() +d) / (d +1u)
    val cs = Matrix(dMsg.pad(d+1u).toDoubleArray(), k)
    val encoded = encode(xs, d.toUShort(), cs)
    val eMsg = encoded.toList().map { it.roundToInt() }
    println("Kodierte Nachricht: $eMsg")

    for (p in listOf(0.0, 0.05, 0.1, 0.15, 0.2)) {
      println("%.0f%% Rauschen:".format(p*100))
      val ys = Matrix( eMsg.map { (it+noise(p)).toDouble() }.toDoubleArray(), k)
      val decoded = decode(xs, d.toUShort(), ys)
      println("Dekodierstatus: ${decoded.second}")
      val recMsg = decoded.first.toList().map { it.roundToInt().toByte() }
        .encodeToByteArray().toString(Charsets.UTF_8)
      println("Erhaltene Nachricht: $recMsg")
    }
  }

  private val random = Random(System.currentTimeMillis())

  fun noise(p :Double) = if (random.nextDouble()<p) random.nextInt(-20,20)  else 0

  private fun List<Double>.pad(d :UInt) :List<Double> {
    val excess = size % d.toInt()
    if (excess==0)
      return this
    return this + (excess until d.toInt()).map { 0.0 }
  }

Und schließlich brauchen wir noch die Kodiervorschrift:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

  fun encode(xs :List<Double>, d :UShort, cs :Matrix) :Matrix {
    val result = Matrix(DoubleArray(xs.size*cs.n.toInt()), cs.n)
    for (c in 0u until cs.n) {
      xs.forEachIndexed { r, x ->
        var s = 0.0
        for (k in (0u..d.toUInt()).reversed())
          s = s*x +cs[k, c]
        result[r.toUInt(), c] = s
      }
    }
    return result
  }

3.2 Funktioniert das auch?

Du solltest vielleicht das obige Programm mit einem einfachen Text probieren. Die NASA (Weltraumbehörde der USA) hat dazu einen Prototypen geschrieben, der ein Bild kodiert, dann mit Rauschen kopiert und das “Übertragene” wieder dekodiert.

Bild 2: Als Beleg, dass ihr Algorithmus tatsächlich Bilder vor Rauschen schützen kann, hat die NASA das berühmte Bild der Mona-Lisa mit Rauschen wie auf 200AE Wegstrecke simuliert einmal direkt übertragen und einmal mit dem Reed-Solomon Code (rechts). © 2021 Sun Xiaoli, NASA.

Man kann jetzt natürlich behaupten, dass man auch im linken Bild noch die Frau erkennen kann, aber leider sind die Bilder von fernen Planeten nicht so leicht zu entziffern. Aufgrund der extrem ungleichmäßigen Beleuchtung kann es große Kontraste und scharfe Hell-Dunkel-Kanten geben und erst wenn das gesamte Bild nahezu fehlerfrei entschlüsselt ist, kann man versuchen, das aufgenommene zu verstehen.

PS: Es gibt natürlich auch noch weitere Anwendungen: Neben den Laser-Disks (CD, DVD, BD) auch das Digitalradio (DAB) sowie Digitalfernsehen.

Weiterführende Literatur

[1] Wikipedia: wiki > Reed-Solomon-Code.

[2] J. Cepelewicz: How Mathematical Curves Power Cryptography, Quantamagazine 2022.

[3] S.B. Wicker, V.K. Bhargava: Reed Solomon Codes Applications, Wiley, 1999, ISBN 0-7803-5391-9.